この記事ではEZRによるコクランのQ検定とその後の検定の方法を解説します

最後に問題もあるので勉強した成果が試せますね!
準備をしよう
EZRをまだインストールしていなかったり、基本操作がわからなかったり。そもそも何がわからないかわからない人は、まず下記の記事を参考にしてください。
また、三群以上の検定の概要についてまとめた記事もあるので参考にしてください。1度は目を通しておくことをお勧めします。
練習用のEZR用データセットを使っていきます。下記からダウンロードしてください。データセットについての詳細は関連記事を参考にしてください。

それではEZRを起動し、【ファイル → 既存のデータセットを読み込む】からダウンロードした「高度解析用データ」を読み込みましょう!
EZRでやるコクランのQ検定+その後の検定
コクランのQ検定の概要
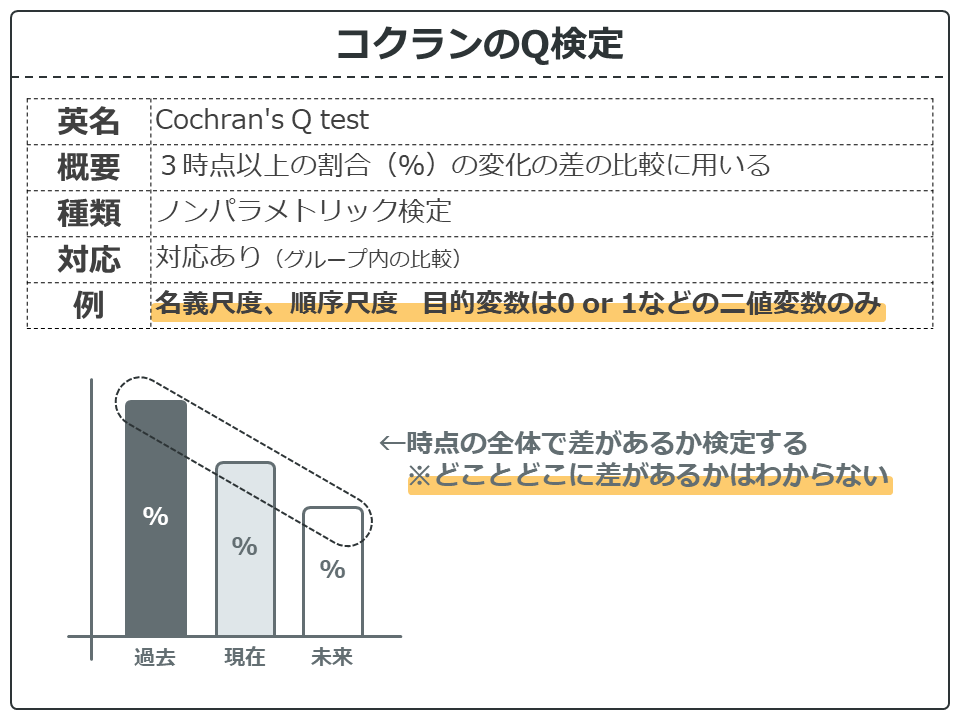
検定手法の概要です。コクランのQ検定は対応のある3時点以上の割合の差の検定を行うノンパラメトリック検定です。3時点とは【過去】【現在】【未来】のようなことです。
また、この検定だけでは、どことどこに差があるかまではわかりません。
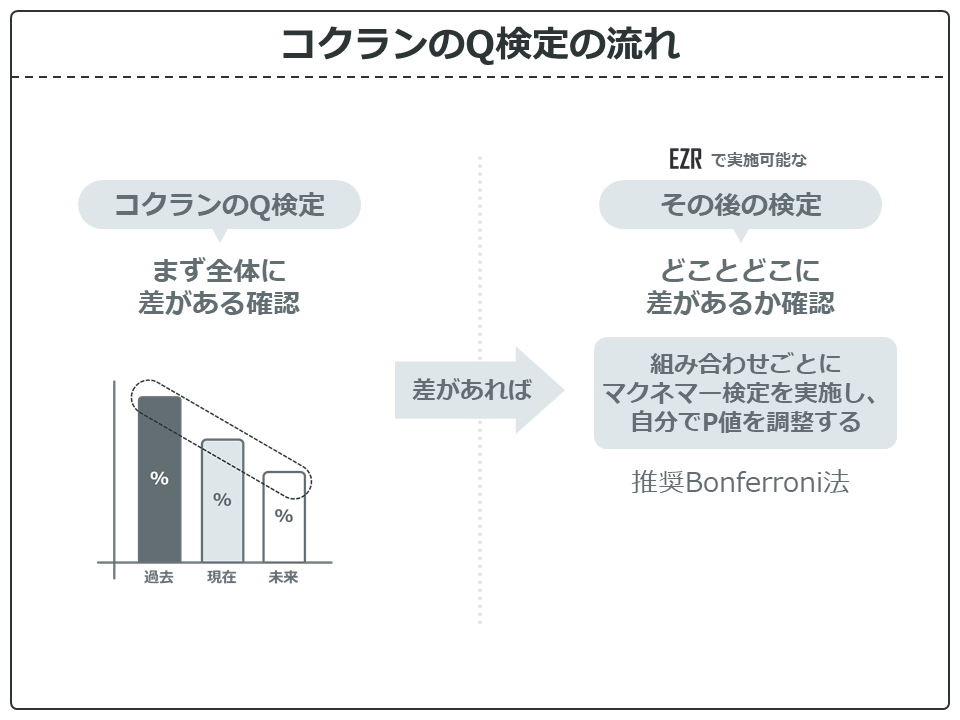
コクランのQ検定の流れです。
まずはコクランのQ検定のP値を求めます。P値が有意水準未満(P<0.05)であれば、全体に差があることがわかります。
全体に差があれば、どことどこに差があるかその後の検定を行いましょう。
しかし、EZRのコクランのQ検定ではその後の検定を自動で行うことができません。仕方がないので、一番簡単なBonferroni法で行います。Bonferroni法は電卓があれば簡単に計算できます!
この記事ではBonferroni法で紹介していきます。
コクランのQ検定+その後の検定(Bonferroni法)のEZR操作手順
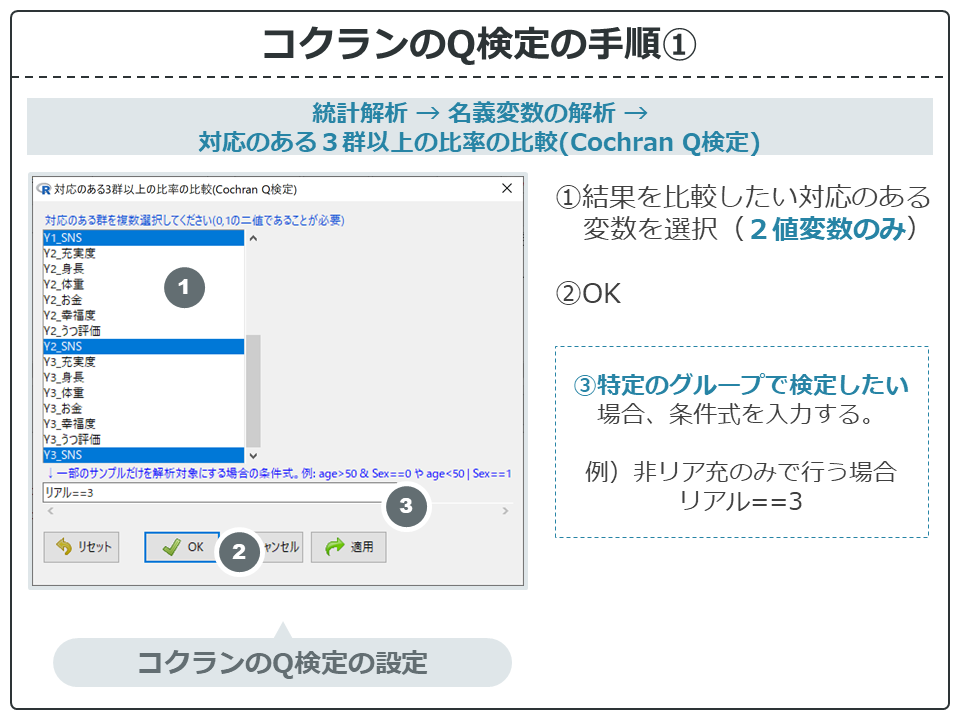

【統計解析 → 名義変数の解析 → 対応のある3群以上の比率の比較(Cochran Q検定)】から設定画面を開きます。
コクランのQ検定の設定からでは、その後の検定はできません。そこで、コクランのQ検定の後に組み合わせごとでマクネマー検定を行いBonferroni法(手計算)でP値を補正します。
Bonferroni法はとっても簡単で、比較した群・グループ数(または時点数)に応じた係数をP値に掛けるだけです。この係数は組み合わせの数と同じ値です。
上の画像を参考に、選択していきます。選択を終えたら【OK】を押しましょう。結果が出力されます。
非リア充(リアル==3)の、プログラム実施前のY1_SNS、プログラム実施後のY2_SNS、Y3_SNSの使用率の変化の差を検定してみよう(その後の検定はBonferroni)
- ① Y1_SNS、Y2_SNS、Y3_SNSを選択
- ③ リアル==3 を入力
- ② OKをクリック
- 組み合わせごとでマクネマー検定
- Bonferroni法で補正する
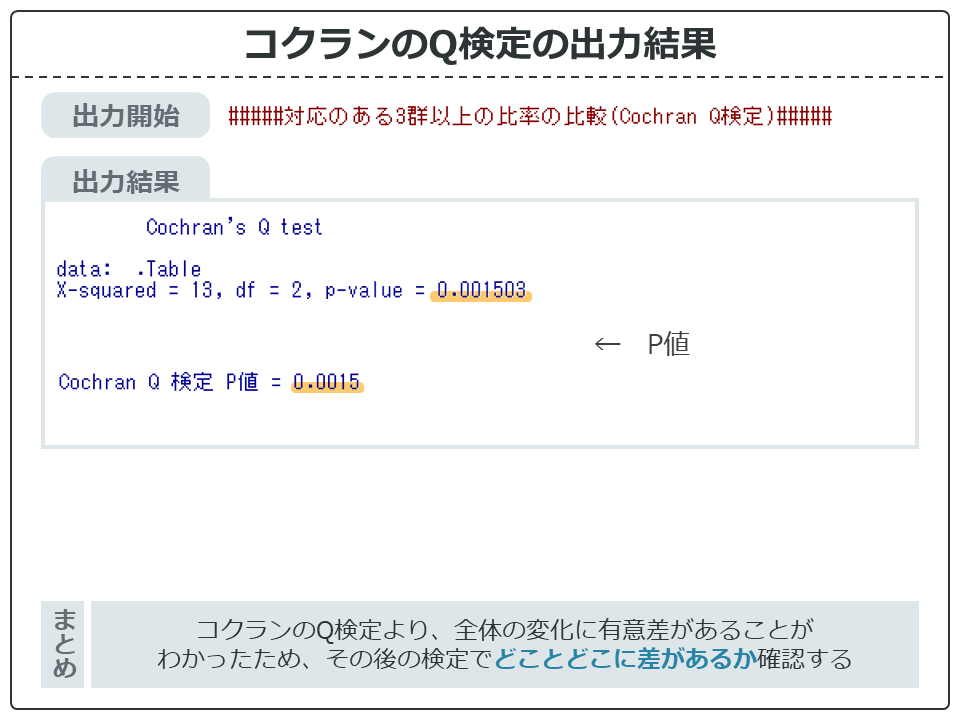
たくさん出力されるので、まずは出力開始の部分を探しましょう。そこから出力されているので、順番に下に見ていきます。検定の結果はデフォルトでは青字で出力されています。
出力結果からコクランのQ検定のP値を探します。
P値は0.001503で、有意水準の0.05(5%)を下回っているので有意であることが分かりました。つまり、時点全体のどこかに差があることがわかりました。
続いて、どことどこに差があるか、組み合わせごとにマクネマー検定を行い、Bonferroni法で補正しましょう。
マクネマー検定の方法は関連記事を参考にしてください。

組み合わせごとでマクネマー検定を行い、P値を求めます。
そして、Bonferroni法による補正を行います。今回は3グループで組み合わせの数が3なので係数3を掛けます。有意差が見られたのは1年目と3年目のSNS使用率のみでした。
また、残念ながら、コクランのQ検定もマクネマー検定も基本統計量を同時に計算してくれません。仕方がないので【グラフと表 → サンプルのサマリーデータの背景表の出力】から出力しましょう。
今回の結果は「非リア充のSNS使用率はプログラム実施前の1年目は26.7%、実施後の2年目では46.7%、3年目では63.3%であり、1年目と3年目の間に有意な差が見られた(P=0.008)。」となりました。
さらに挑戦してみよう!コクランのQ検定
これでコクランのQ検定は終わりです。せっかくなので下記から練習してみてください。このままのデータセットで練習できます。
また、一部の問題は条件式を利用するので、下記の記事から勉強しておくことをお勧めします。