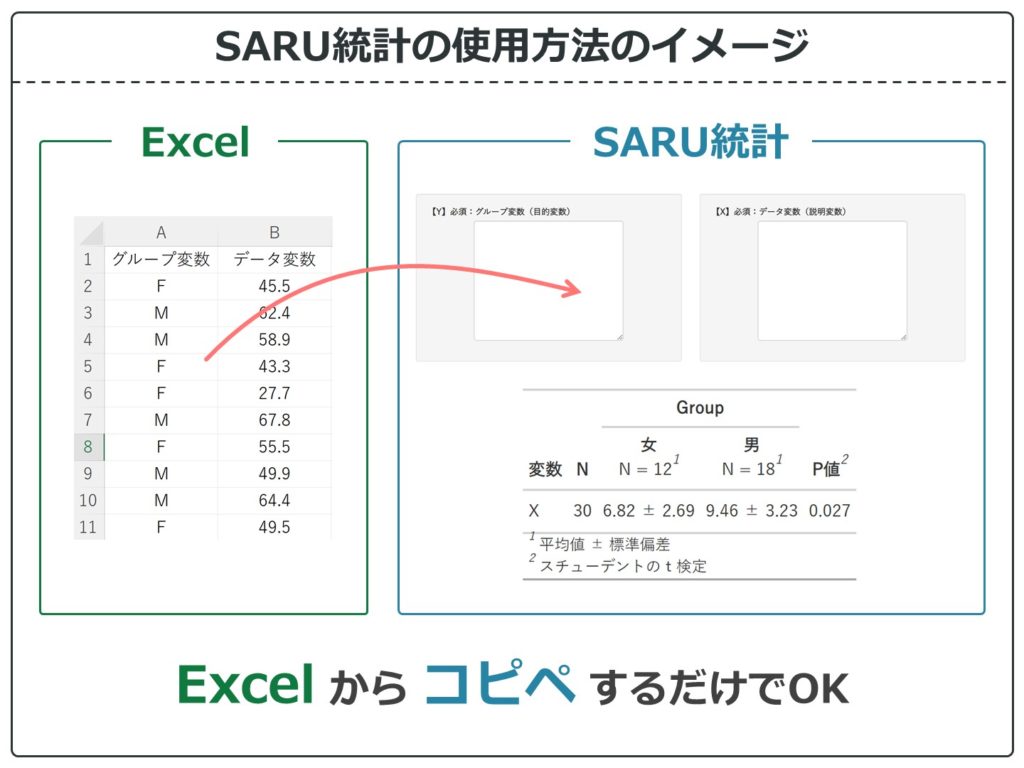
SARU統計は、統計ソフトRが使える無料のオンラインツールです。Excel等のデータさえあればコピペですぐに解析できます。また、サルのために作られているので簡単・無料です。計算はすべてRで行われているので論文や学会発表にも使えます。この記事にサッと目を通して解析しちゃおう!
サルでもわかるし実践できるフィッシャーの正確検定の紹介です。
サルとちんぱんがフィッシャーの正確検定をわかりやすく紹介してくれてます。YouTubeを見れば10分足らずであなたも解析できるようになります。
こんなに簡単に検定できます
実際にYouTubeで検定している部分だけを見る場合はここから。でもサルとちんぱんが喜ぶから最初から見てあげてね。
サルでもわかるフィッシャーの正確検定
動画の内容を簡単にテキストで紹介しておきます。動画の概要確認や資料としてお使いください。動画の方がより詳しく説明しています。
今回もサルとちんぱんでどちらの方がバナナを好きかもめているようです。

好き嫌いのような嗜好性は、段階評価、つまり順序尺度でデータを取得することができます。この場合は符号付順位和検定です。
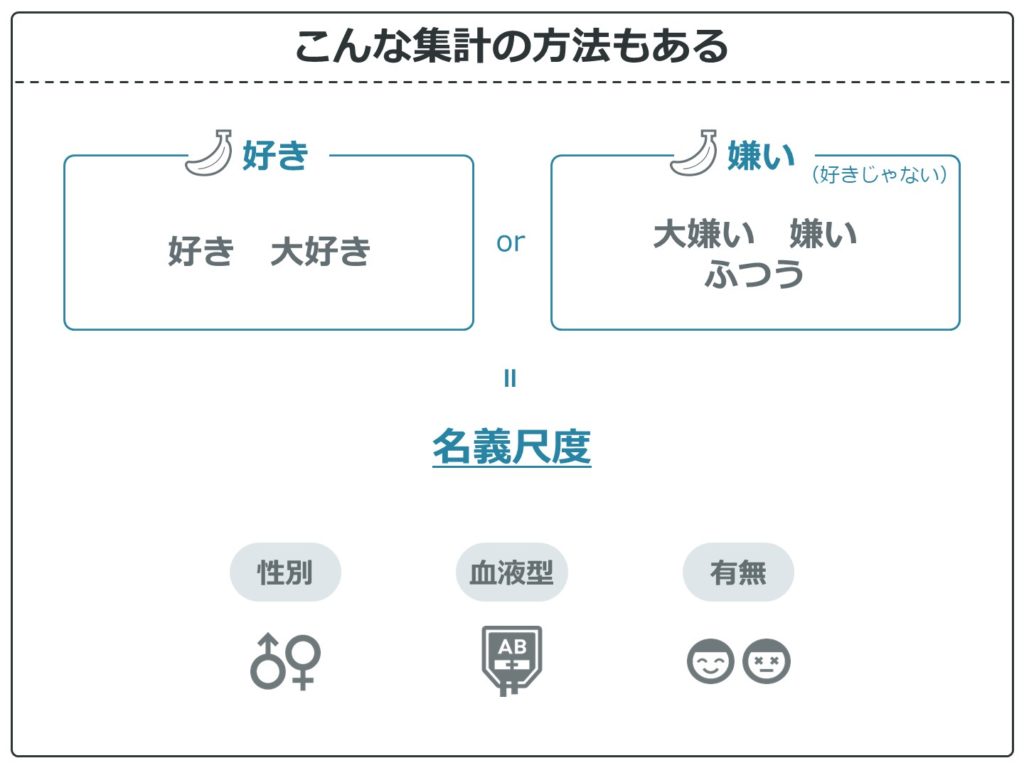
順序尺度データを、このように「好き」か「嫌い」かの二値に分けることができます。こうすると名義尺度としてデータを扱うことができ、解析方法も変わってきます。
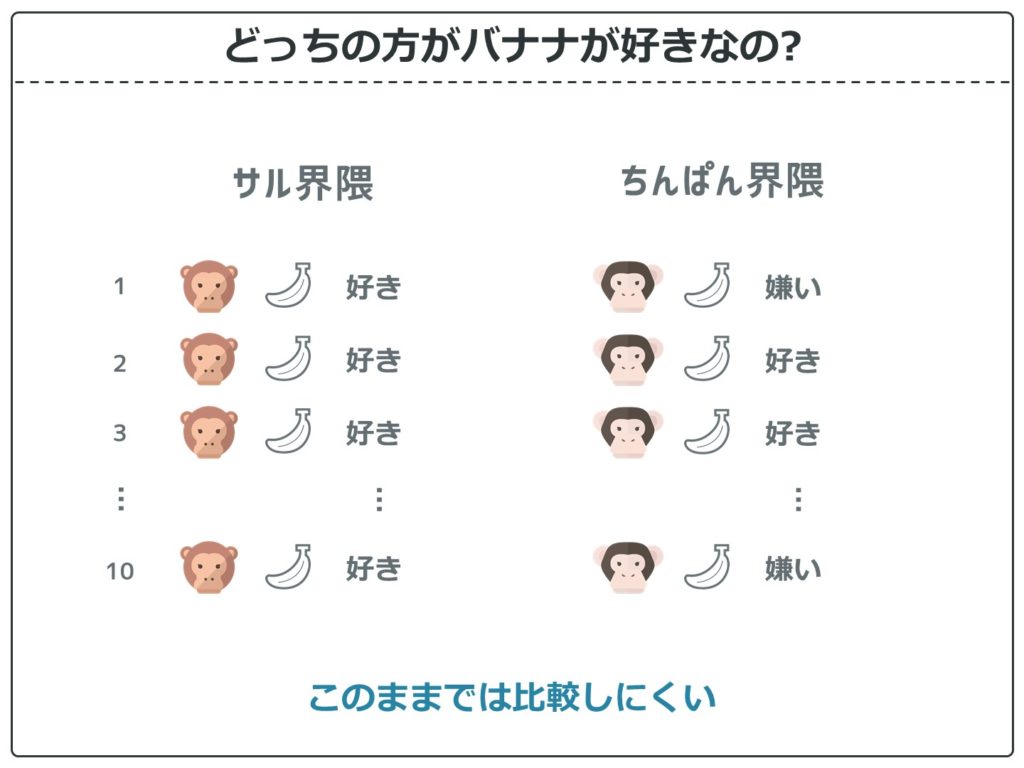
それではサル界隈とちんぱん界隈から10匹ずつ協力してもらい、バナナの嗜好性を調査しました。
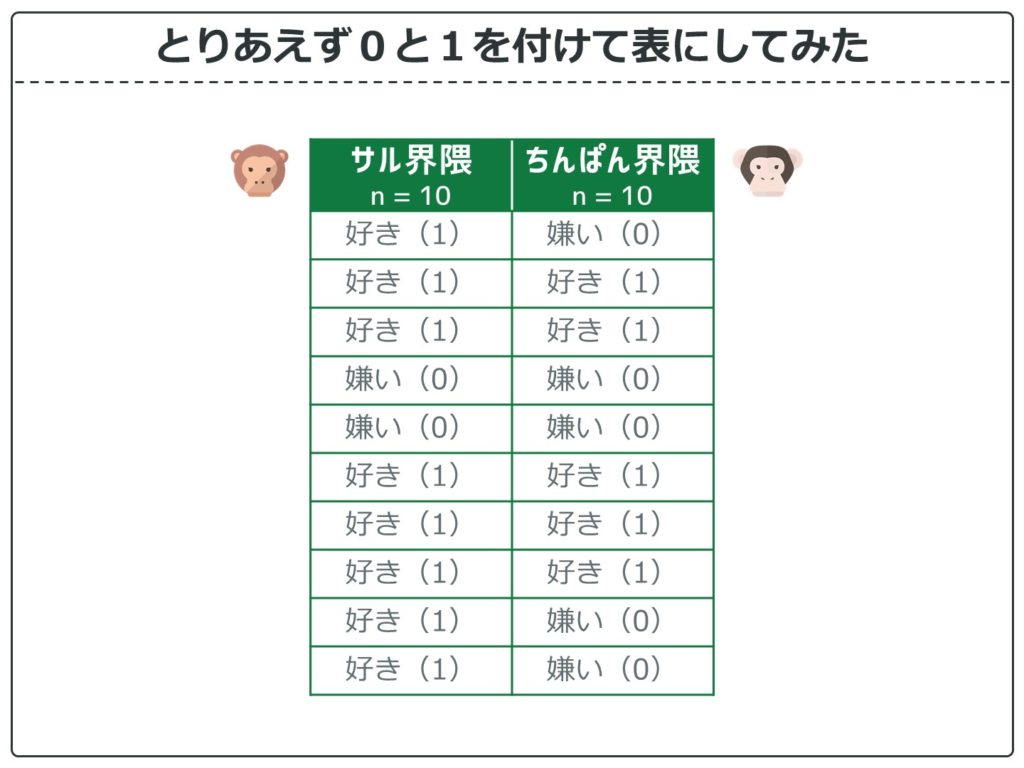
好きには1を、嫌いには0を付けて表にしてみます。
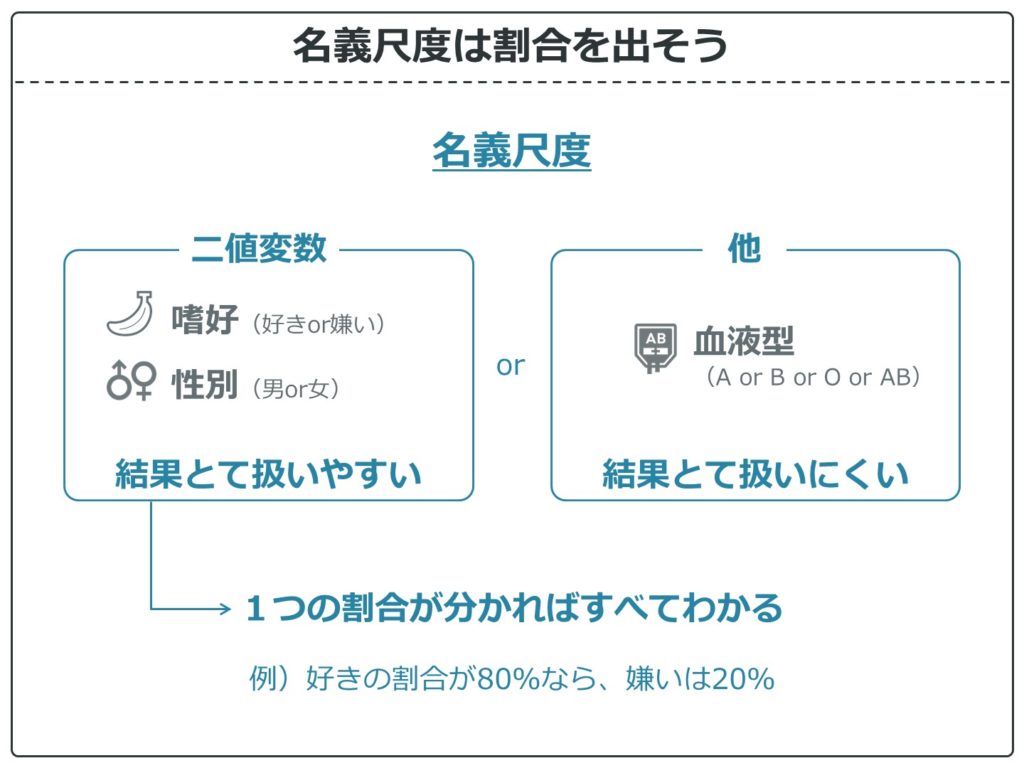
名義尺度の中でも2つの値しかないものを二値変数(二値データ)といいます。
二値変数の方が結果として扱いやすいです。
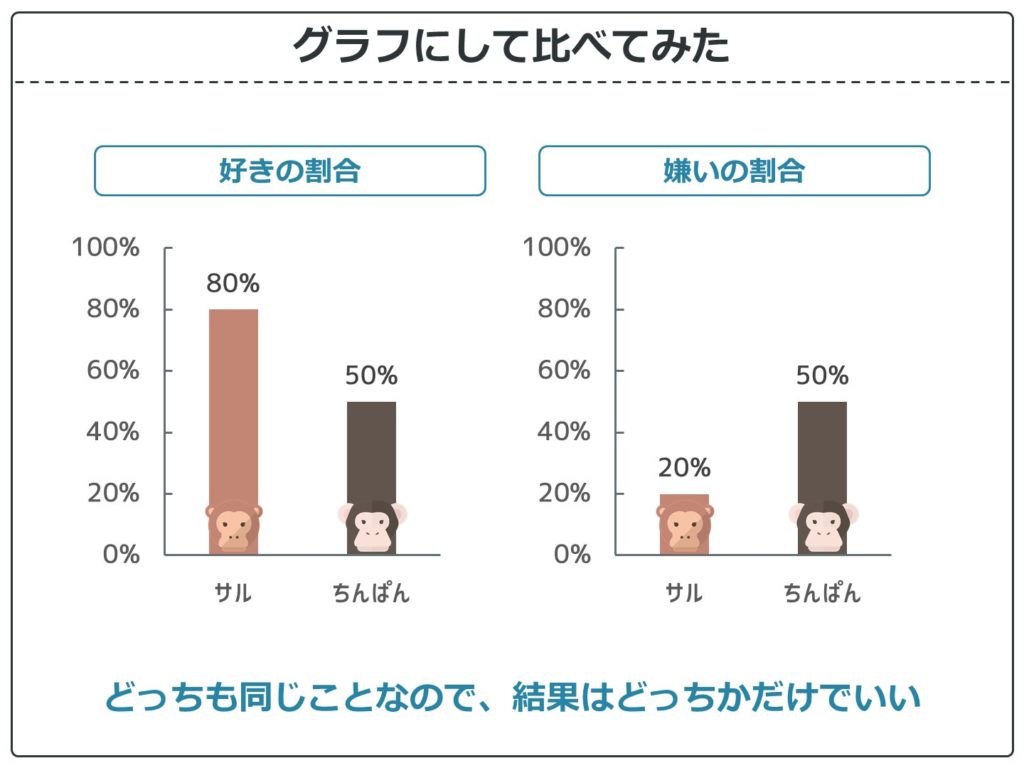
サル界隈とちんぱん界隈のバナナの好きまたは嫌いの割合をグラフにしてみました。
このように二値変数は割合を算出するとわかりやすいです。また、二値変数の場合はどちらか一方の結果だけ示せば、もう一方はわかるので示す必要がありません。
研究の目的になる方の割合を示しましょう。
割合の差の検定について
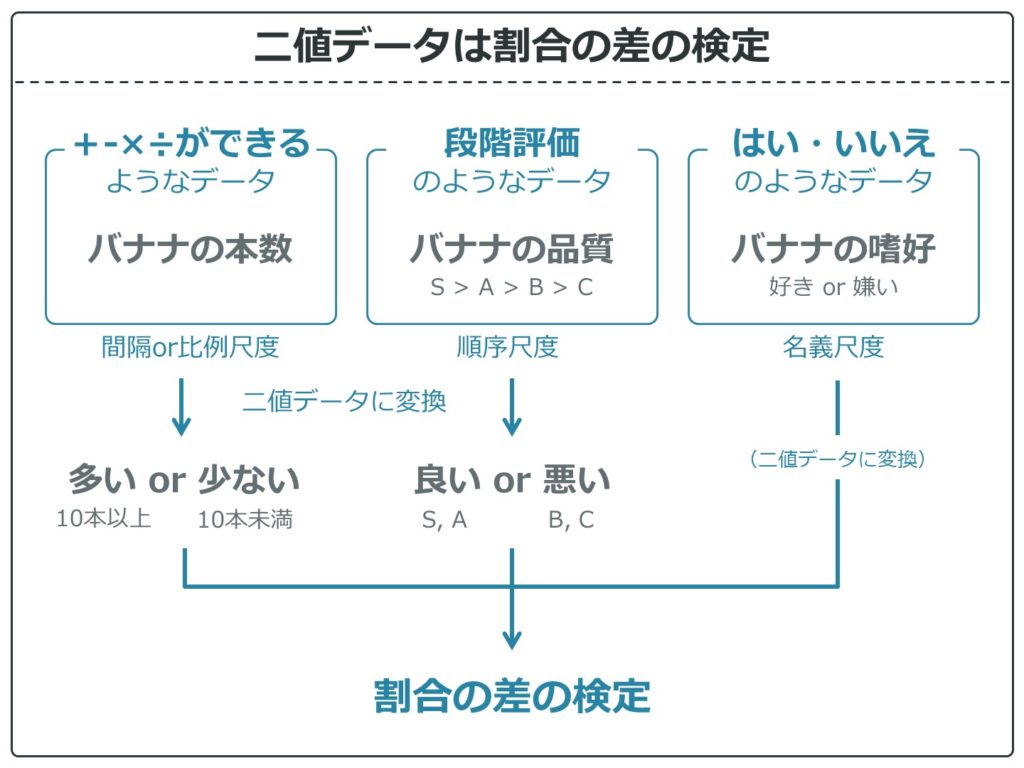
二値データは割合を計算できるので、割合の差の検定を行うことができます。
実は、どんな尺度でも二値データに変換することができるので、実際はどんな変数でも割合の差の検定を行えます。
例えばバナナの本数のような間隔・比例尺度でも、カットオフ値を設けて2分類すれば二値変数として扱うことができます。検査値から病気の分類を行い、有病率を求めて比較するといったように、よく使われるテクニックです。
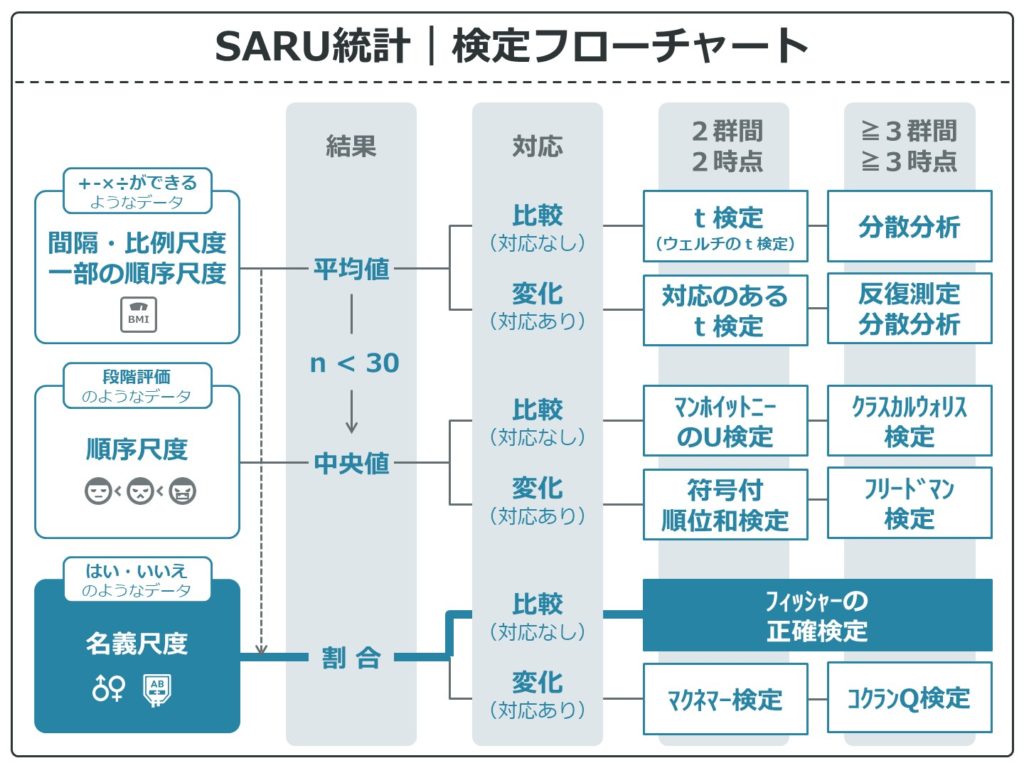
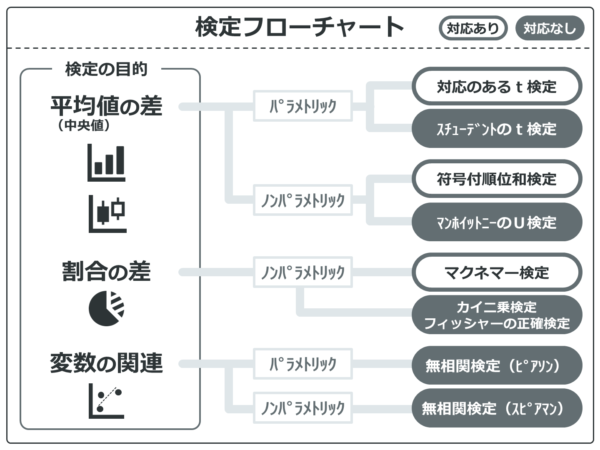
検定を選択するためのフローチャートです。
名義変数は左下からスタートし、割合を結果として扱います。また、今回はサルとちんぱんの比較のようにグループ間の「比較」なので比較のフローをたどっていきます。
このようなグループ間の比較のことを「対応なし」ともいうので覚えておきましょう。
フローをたどると、フィッシャーの正確検定が選択されました。

とりあえず、2グループ間の比較で、割合が出せる二値データはフィッシャーの正確検定を使いましょう。
ただ、フィッシャーの正確検定は3グループ以上の比較でも使用できます。

フィッシャーの正確検定の例を挙げておきます。
SARU統計で実際にフィッシャーの正確検定をやってみる
動画では実際にSARU統計を使ってフィッシャーの正確検定を実施しています。
ネットにつながるパソコンやスマホがあれば他に用意するものはなにもありません。よかったら実際にSARU統計を使ってみてください。

結果です。SARU統計では論文のような表が結果として出力されます。そのほか、Rの実際の出力も出るので、RやEZRの勉強にもなったりします。
サルのバナナが好きな割合は80%であり、ちんぱんの50%と比較して有意な差はなかった(P = 0.350)といった結果でした。
また、二値データは表裏一体のような関係であるため、どちらの結果で書いてもP値は同じ値になります。
今回はサルとちんぱんのバナナの好きな割合に差はなかったようですね。
まとめ