SARU統計は、統計ソフトRが使える無料のオンラインツールです。Excel等のデータさえあればコピペですぐに解析できます。また、サルのために作られているので簡単・無料です。計算はすべてRで行われているので論文や学会発表にも使えます。この記事にサッと目を通して解析しちゃおう!
サルでもわかるし実践できる対応のないのt検定(スチューデント/ウェルチ)の紹介です。
サルとちんぱんが対応のないのt検定(スチューデント/ウェルチ)をわかりやすく紹介してくれてます。YouTubeを見れば10分足らずであなたも解析できるようになります。
こんなに簡単に検定できます
実際にYouTubeで検定している部分だけを見る場合はここから。でもサルとちんぱんが喜ぶから最初から見てあげてね。
サルでもわかる対応のないのt検定(スチューデント/ウェルチ)
動画の内容を簡単にテキストで紹介しておきます。動画の概要確認や資料としてお使いください。

サルとちんぱんのどちらが給料(バナナ)が多いでしょうか?もちろんちんぱんの方が多いです。

では、サル界隈とちんぱん界隈の各30匹ずつのデータを見てみましょう。このままでは比較しにくいです。
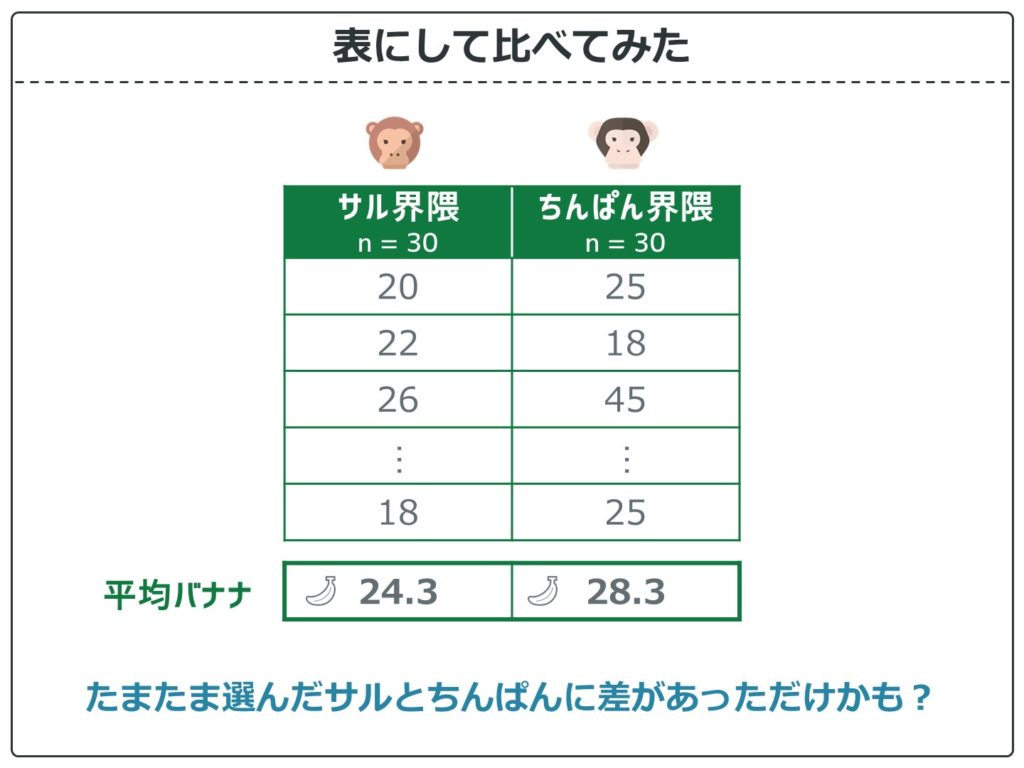
表にまとめて集計してみました。
サル界隈の平均バナナが24.3本で、ちんぱん界隈が28.3本と差があるように見えます。
ただ、これはたまたま選んだサルとちんぱんに差があっただけかもしれません。このように、平均値の差が偶然かどうかを調べるためには平均値の差の検定を行う必要があります。
平均値の差の検定について
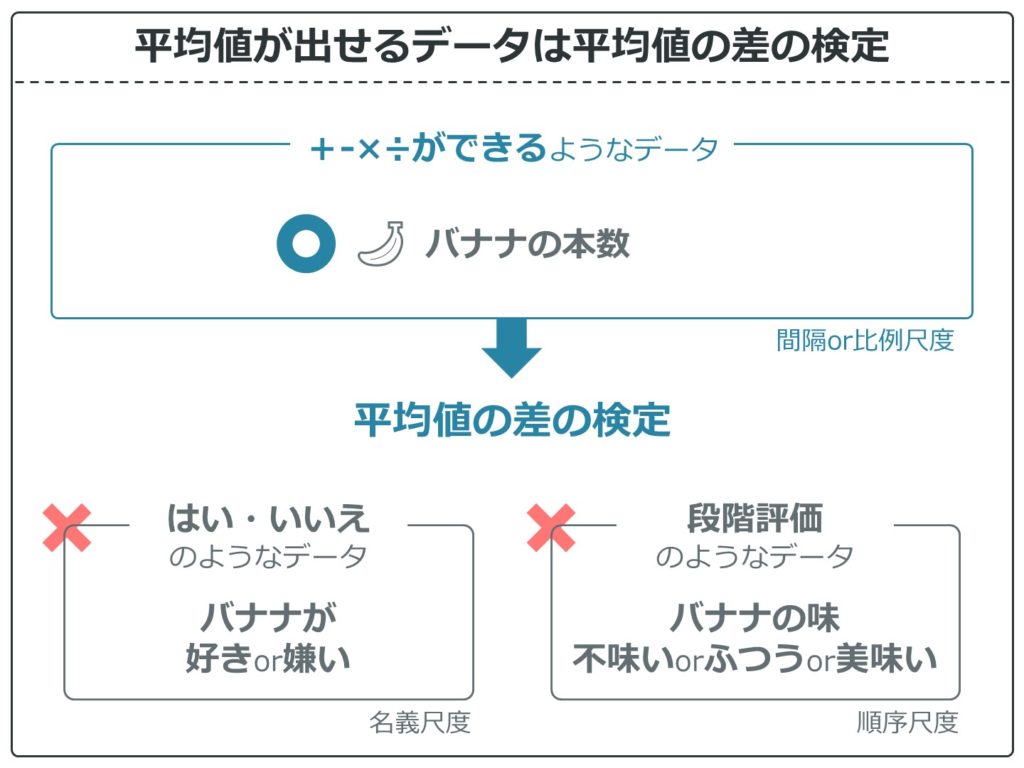
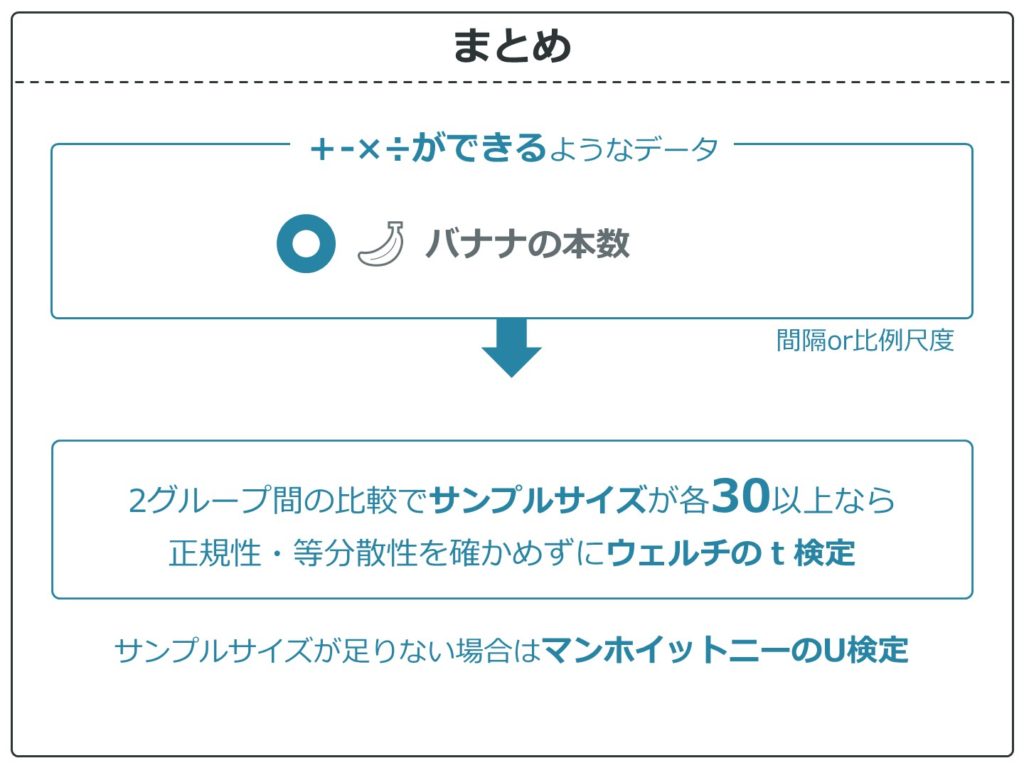
平均値を出すためには四則演算がいります。バナナの本数のような間隔・比例尺度データであれば平均値の差の検定が行えます。
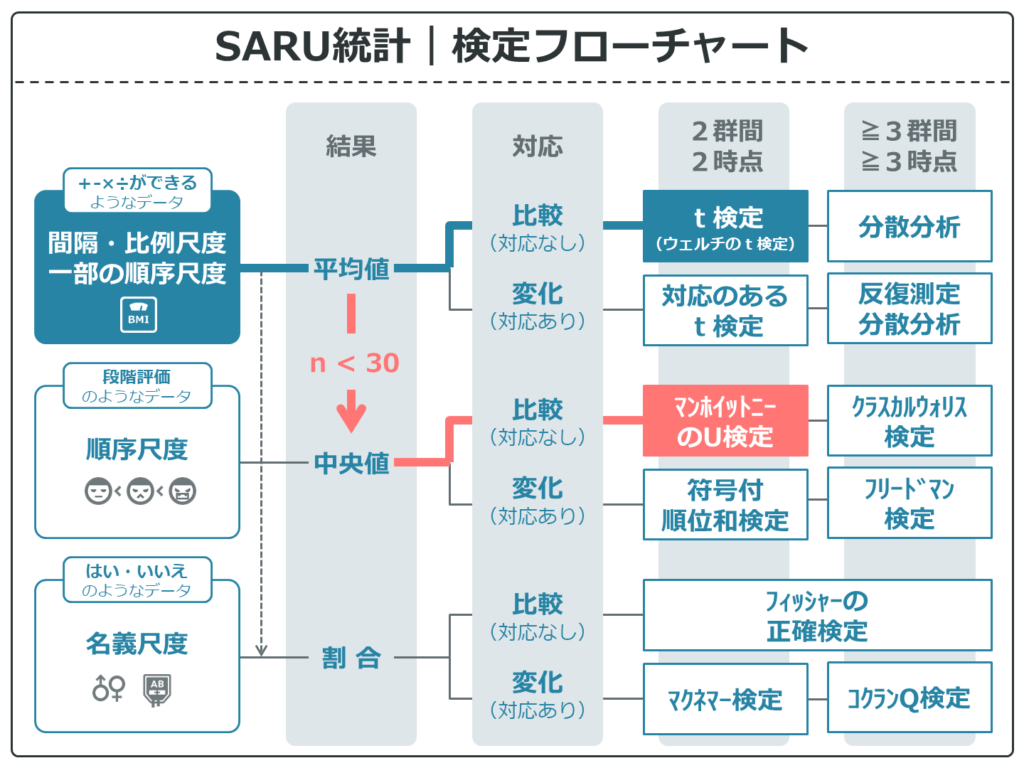
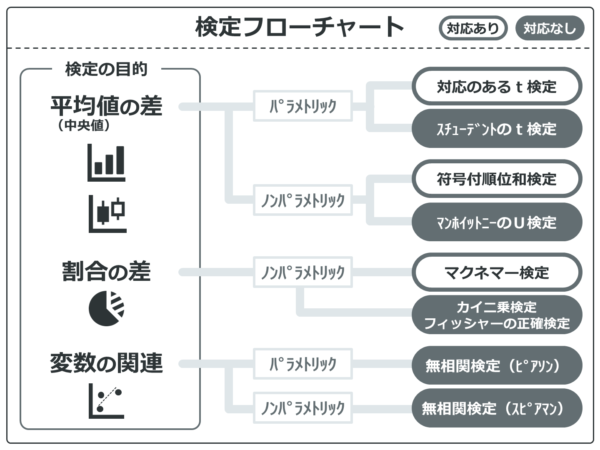
検定フローチャートでみてみましょう。
間隔・比例尺度は平均値が出せます。また、今回は2グループ間の比較(対応なし)となるためt検定が選択されます。
サンプルサイズが30未満だと、マンホイットニーのU検定を使うことになります。

とりあえず、2グループ間の比較でサンプルサイズが各30以上なら正規性・等分散性を確認せずにウェルチのt検定を使って大丈夫です。
正規性や等分散性というのはt検定を使うためのデータの条件のようなものですが、サンプルサイズが30以上であれば正規性は問題ないとされ、等分散性についてはウェルチのt検定は必要ないため、この選び方をしていれば難しいことは考えなくてすみます。
もし、サンプルサイズが足りない場合は、マンホイットニーのU検定を使いましょう。
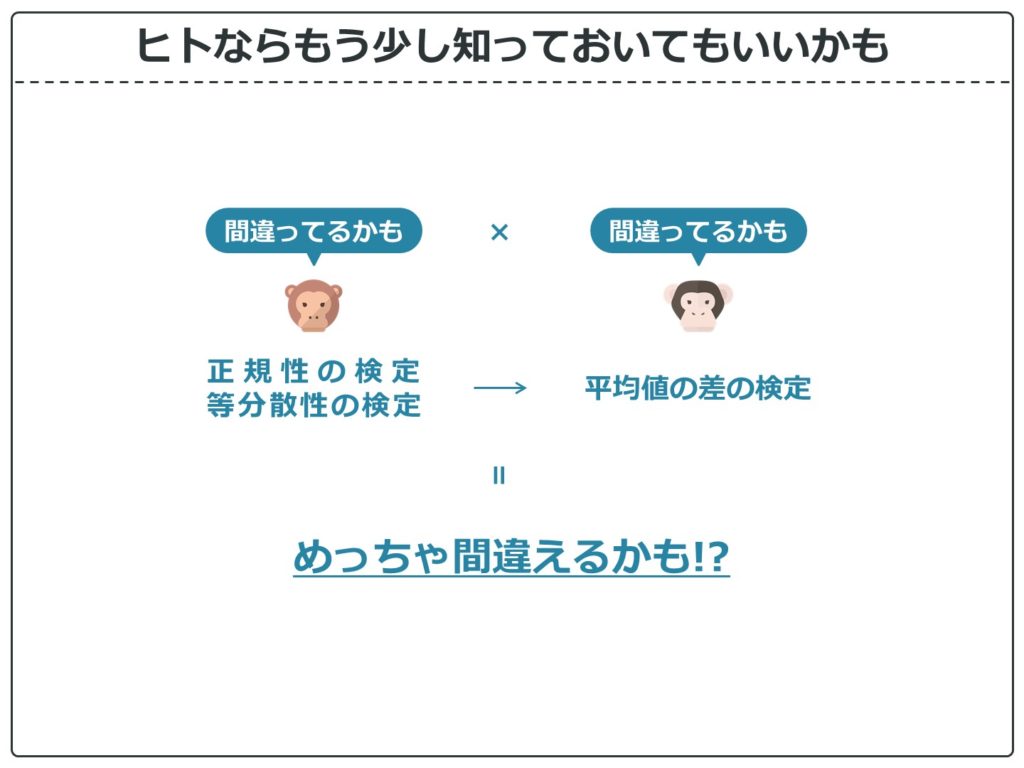
よく参考書などで、正規性の検定を行い、次に等分散性の検定を行ってから、スチューデントt検定かマンホイットニーのU検定かを行うように紹介されています。
ただ、これは問題も指摘されていて、正規性や等分散性の検定も間違っている確率があります。その上でさらに間違う可能性のあるスチューデントのt検定を行うと、想定よりも間違える確率、つまりP値が大きな値になってしまう可能性があるからです。
なので、ここで紹介しているようにサンプルサイズをみて検定手法を選択したり、等分散性の検定をせずにすべてウェルチのt検定を行うような方法もあります。
どれかが絶対にだめというわけではないので、自分の信じてきたやり方や自分の周りのやり方に合わせるといいですね。

対応のないのt検定(スチューデント/ウェルチ)を使う例を挙げておきます。
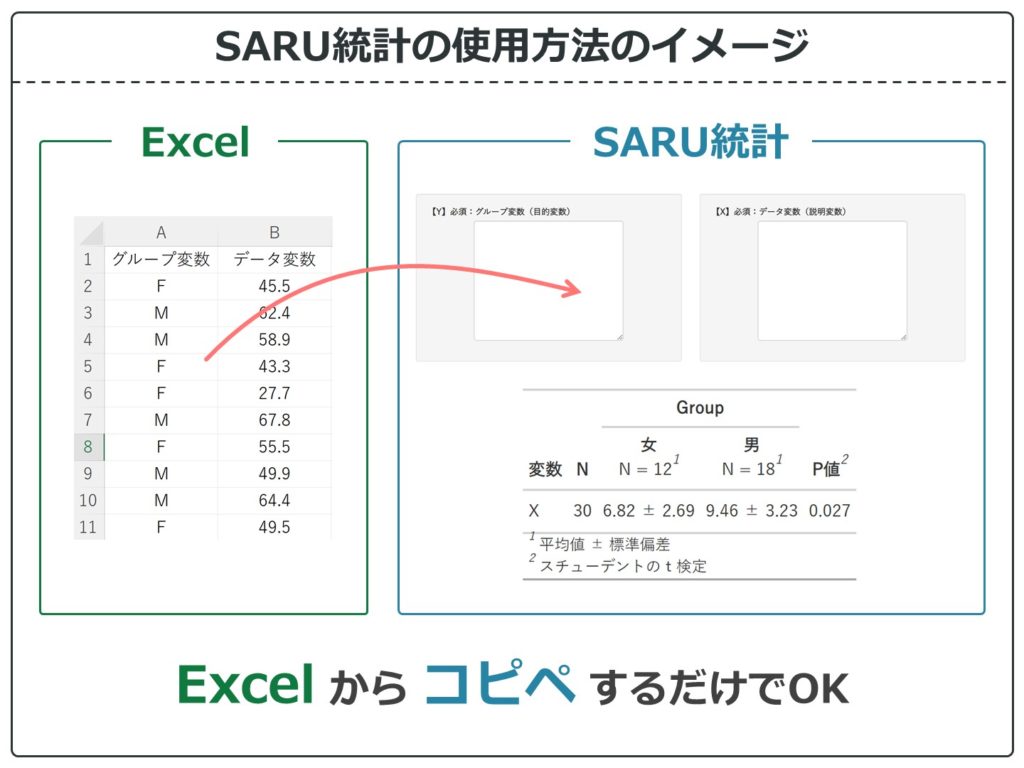
SARU統計で実際に対応のないのt検定(スチューデント/ウェルチ)をやってみる
動画では実際にSARU統計を使って対応のないのt検定(スチューデント/ウェルチ)を実施しています。
SARU統計はスチューデントのt検定の結果も、ウェルチのt検定の結果もどちらも出力されるので、こだわるのであれば自分で選んでください。SARU統計のデフォルトはウェルチのt検定になっています。
ネットにつながるパソコンやスマホがあれば他に用意するものはなにもありません。よかったら実際にSARU統計を使ってみてください。

結果です。SARU統計では論文のような表が結果として出力されます。そのほか、Rの実際の出力も出るので、RやEZRの勉強にもなったりします。
サルのバナナの平均値は24.3±3.2本であり、ちんぱんの28.3±4.7本と比較して有意に少なかった(P < 0.001)といった結果になりました。
統計的に見ても、サルよりちんぱんの方が給料(バナナ)が多かったみたいですね。
まとめ