SARU統計は、統計ソフトRが使える無料のオンラインツールです。Excel等のデータさえあればコピペですぐに解析できます。また、サルのために作られているので簡単・無料です。計算はすべてRで行われているので論文や学会発表にも使えます。この記事にサッと目を通して解析しちゃおう!
サルでもわかる基本的な検定手法の使い分けの紹介です。
サルとちんぱんがわかりやすく紹介してくれてます。YouTubeを見れば10分ちょっとで理解できるようになります。
ゆっくり落ち着いて読みたい方は動画の内容を記事にしてあるので、ゆっくり勉強してみてください。
基本的な検定でできること
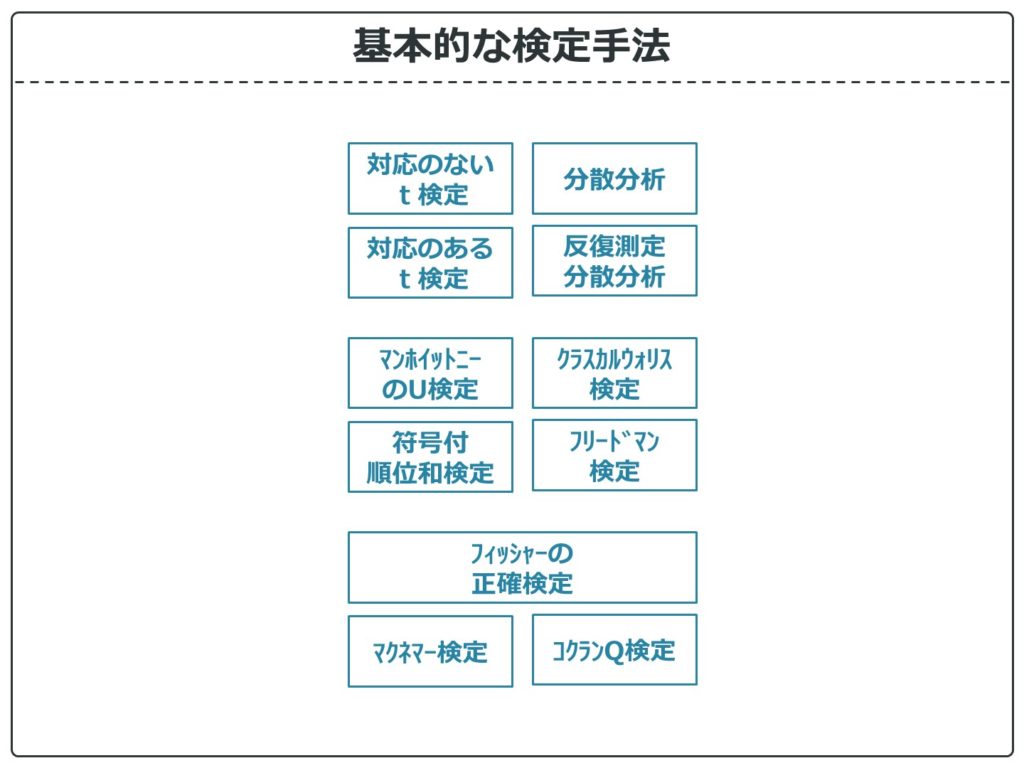
検定手法にはたくさんの種類がありますが、まずはこれくらいが基本的な検定となります。
これを使えるのではなく使い分けれるようになれば、当面は困らないと思います。
実際に使うときは、それぞれの統計ソフトの検定手法ごとの解説を見ながらやればできますが、使い分けが分からないと、何していいかわからないからですね。

では、基本的な検定では何ができるのでしょう?なんでもできちゃう魔法?そんなことはないんです。
基本的な検定でできることは、差があるかどうか確かめることだけ。たったこれだけしかできません。
では差には何があるのでしょうか?
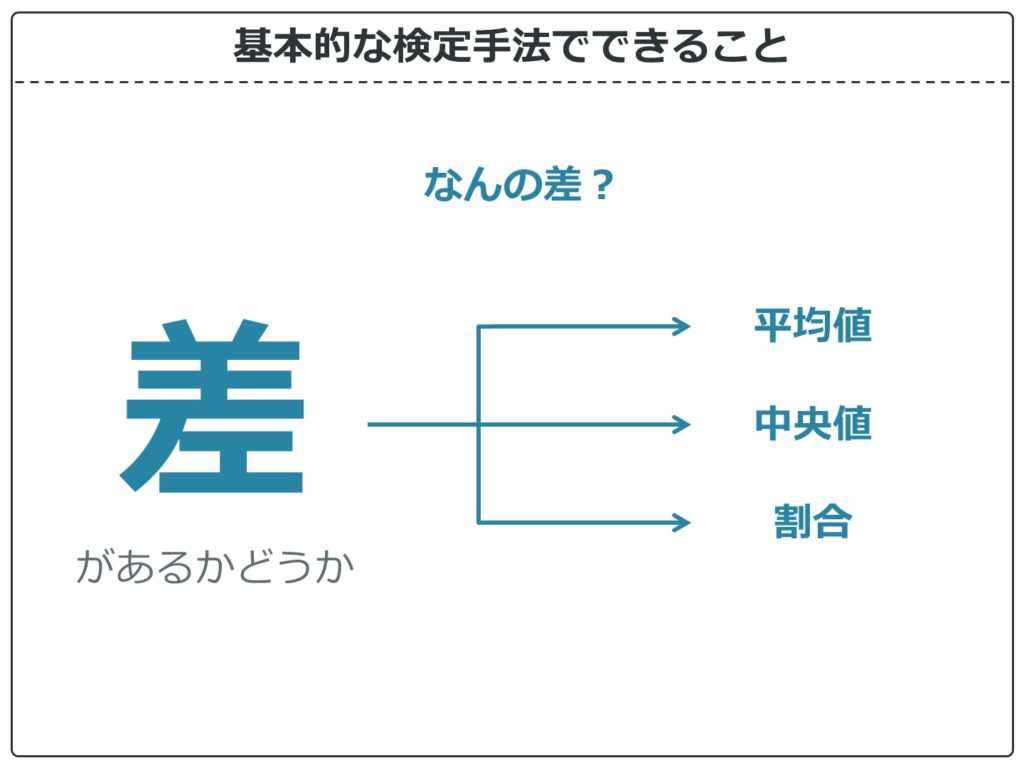
まず、なんの差?ということで、差には平均値と中央値と割合(%)があります。
詳しくはここから。
大事なことですが、検定って平均値と中央値と割合の差くらいしか分からないんです。だから、データを集めるときから、このどれで集計するか考えておくと、どの検定をすればいいか迷わなくなりますよ。
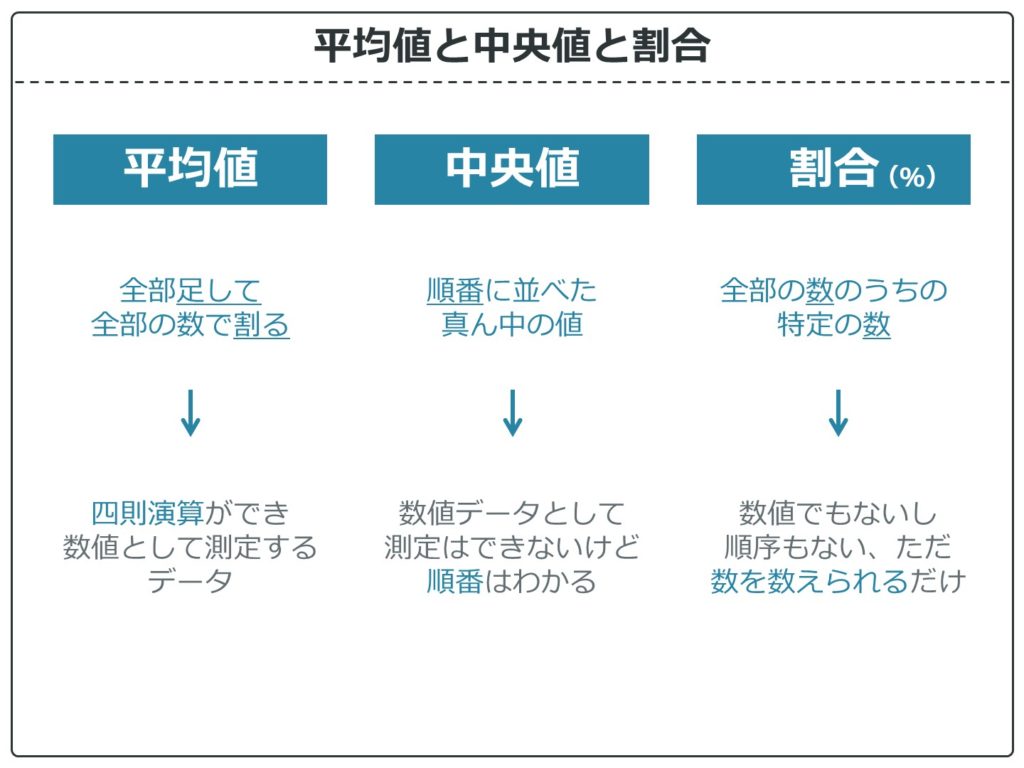
もう少し細かくみておきます。
平均値は、足したり割ったりと、四則演算(+ー÷×)をする必要があります。だからそういった数値のデータは平均値を出しますね。
中央値は、名前の通り真ん中の値なので、順番に並べて真ん中にくる値です。順番さえわかればいいので、数値データのような客観的な値でなくても、人の気持ちとか度合いといった主観的なものでも計算できます。
割合はちょっとイメージに困る人がいるみたいですね。
割合ってのは数が数えられれば計算できます。例えばある教室にいる人数は数えられますね?10人いたとしましょう。そこで質問して手を挙げてもらいます。手を挙げた人数ももちろん数えられます。5人いたとしたら、手を挙げた割合は50%と計算できます。
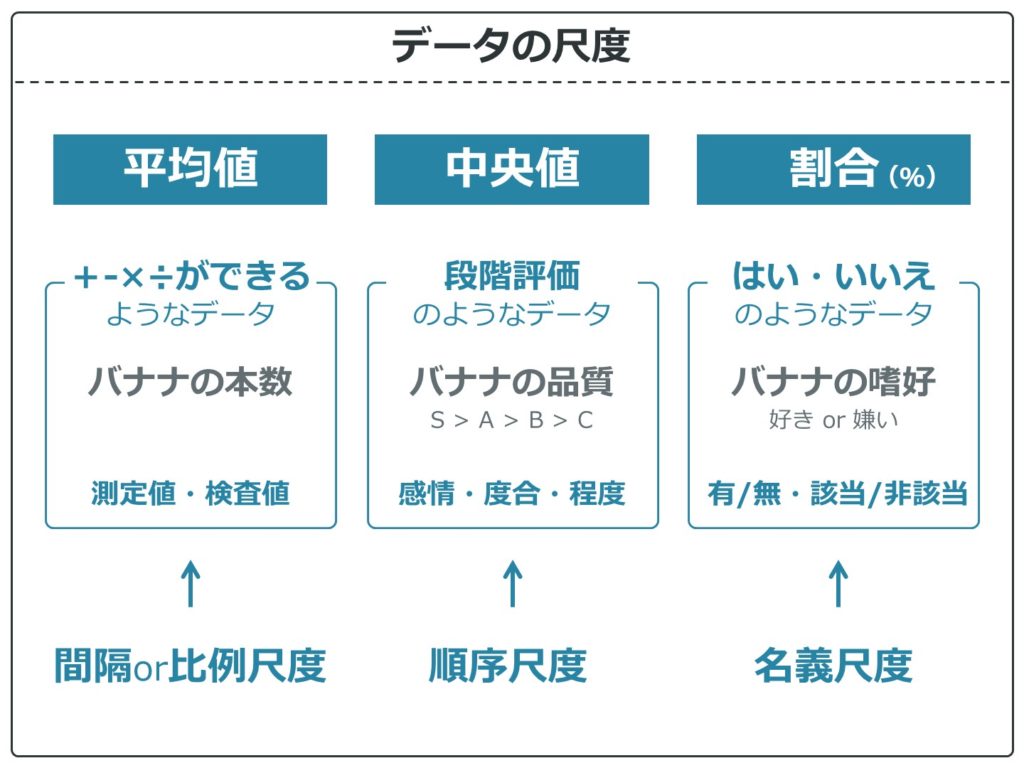
まとめるとこんな感じです。
平均値は測定値や検査値、中央値は感情や度合い、程度といった数値ではないけど順番がわかるもの、割合は「はい/いいえ」のような数しか数えられないものです。
また、平均値が出せるような数値データを「間隔or比例尺度」、中央値を出すような順番データを「順序尺度」、割合を出すようなデータを「名義尺度」と呼びます。
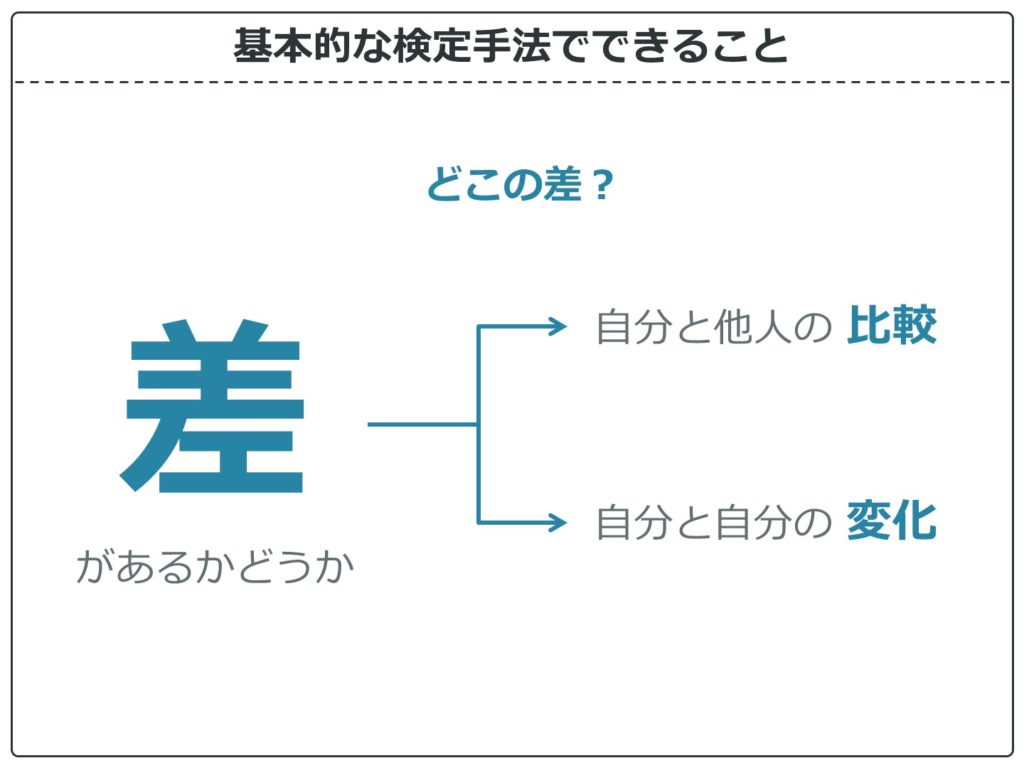
さて、2つめの差はどこの差かということです。
これには「自分と他人の比較」と「自分と自分の変化」を比べた時に生じる差です。
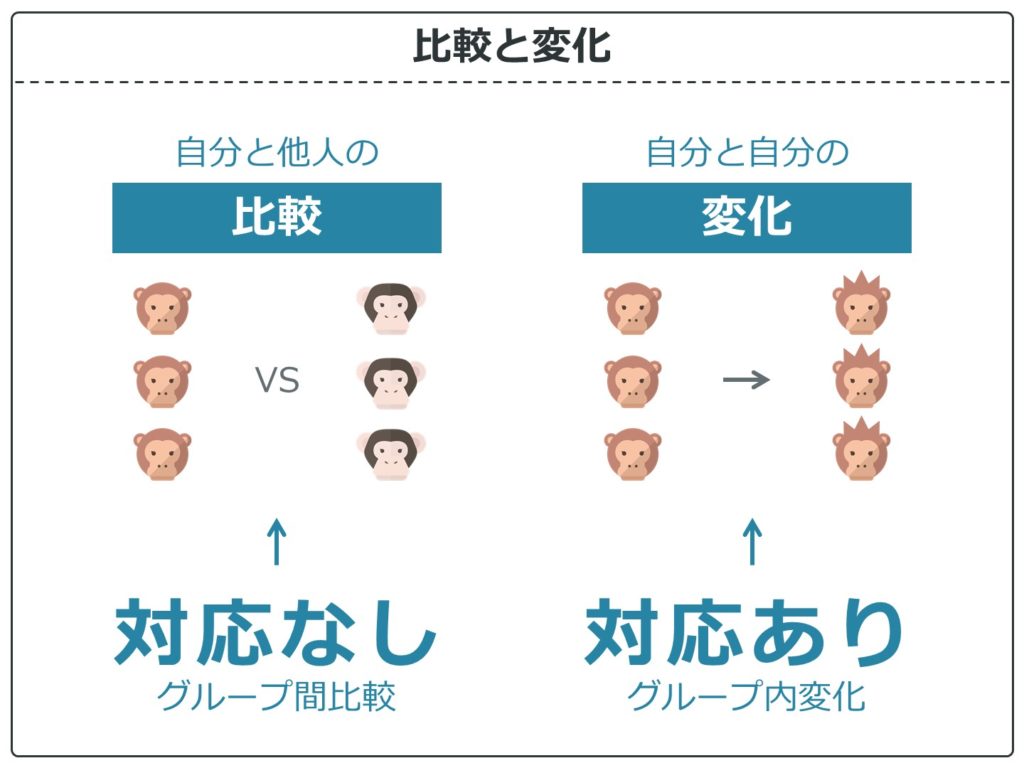
自分と他人のようなグループ間比較のことを「対応なし」といいます。
また、自分と自分の変化のようなグループ内変化を「対応あり」といいます。
そんなに難しいことではないので、これは統計用語、そういうものだと思ってください。
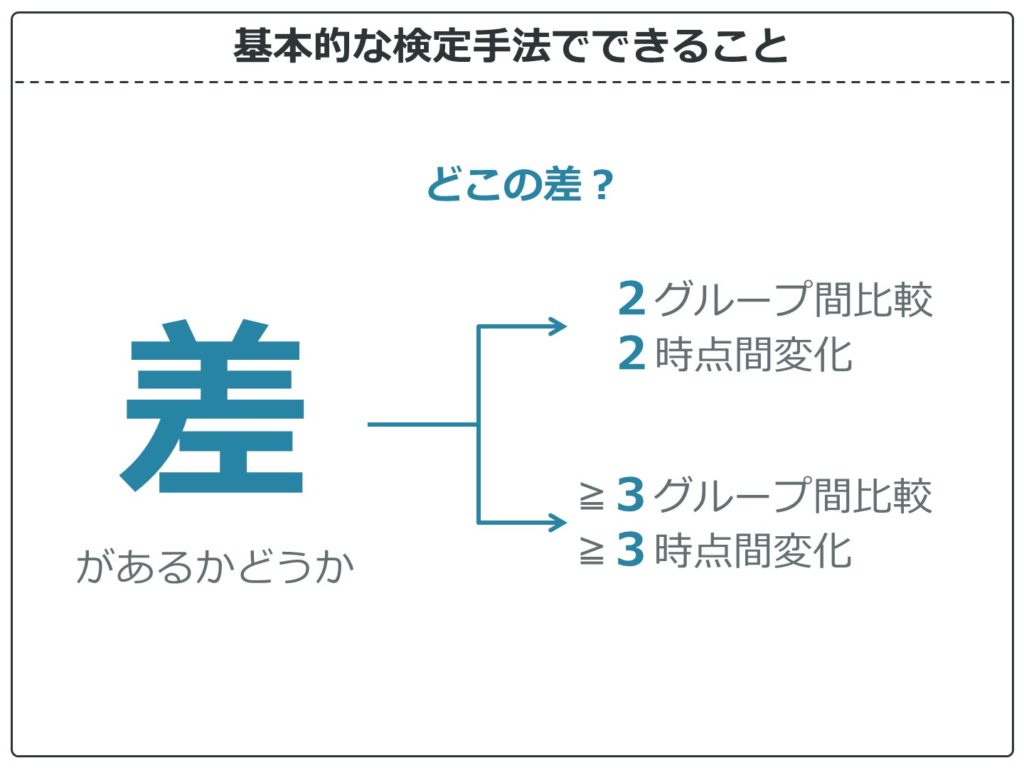
さて、最後の差です。といっても先ほどの「対応」の補足です。
実は、2と3以上で検定手法が変わります。2ってのは2グループ間(対応なし)または2時点間(対応あり)の差のことで、それが3以上になると検定手法が変わります。
そういうものだと思っておきましょう。
検定を使い分けるに覚えておくこと
なんの差?
平均値(間隔・比例尺度)、中央値(順序尺度)、割合(名義尺度)
どこの差?
自分と他人の比較(対応なし)、自分と自分の変化(対応あり)
2群間・2時点と3群間以上・3時点以上は手法が異なる
これだけ。なんかできそうな気がしませんか?
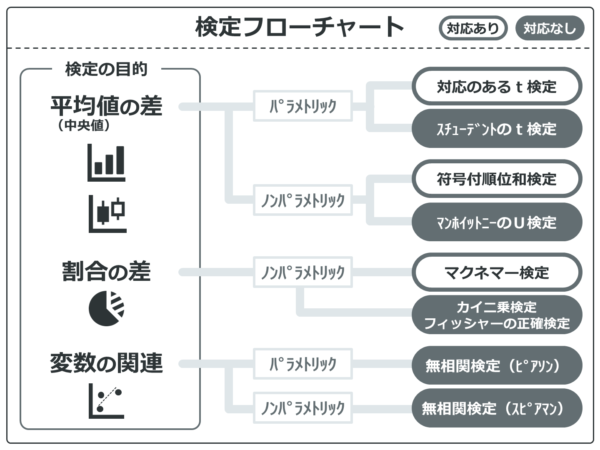
検定フローチャート
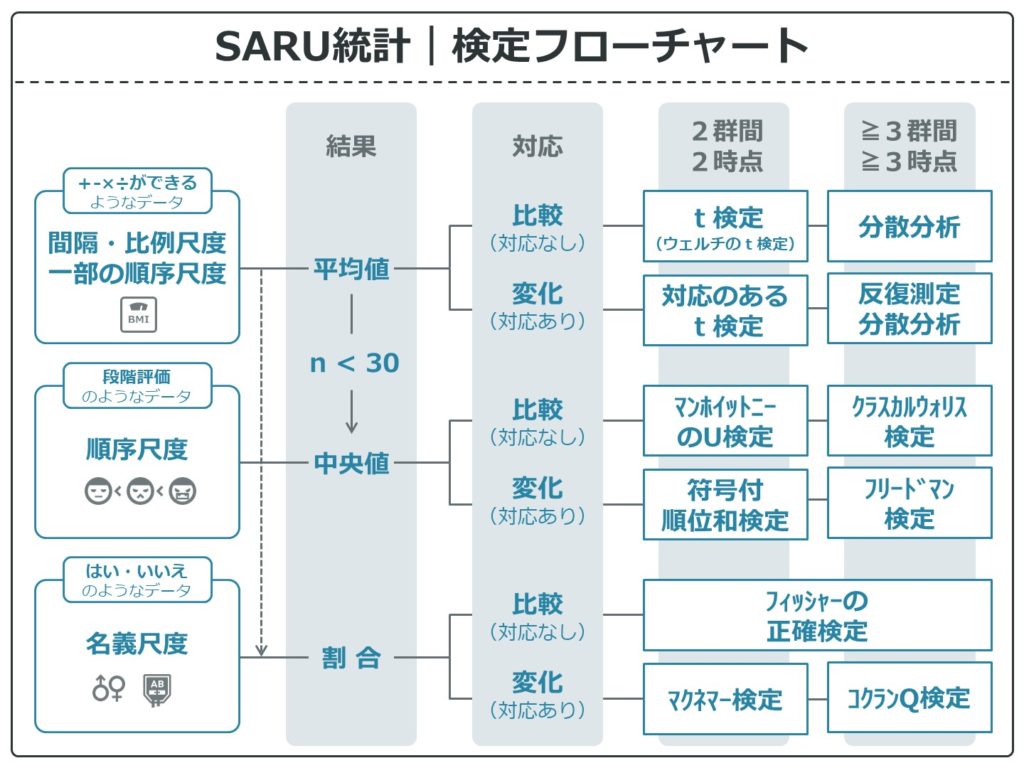
ではここまでの情報と、基本的な検定を組み合わせると、こんなフローチャートになります。フローチャートを辿れば検定手法の名前がわかるので、あとは自分の使っている統計ソフトで検定できます。
ちなみに本サイトにあるSARU統計を使えば、論文でも使える検定結果がインストール不要の完全無料で、しかもオンラインでコピペだけでできちゃうので、よかったら使って下さい。
では、ここまでではまだふわふわしてると思うので、具体的な例もいくつか見てイメージをしっかりと持ちましょう!
こういう時はどの検定?の例
2グループ間比較で平均値の差

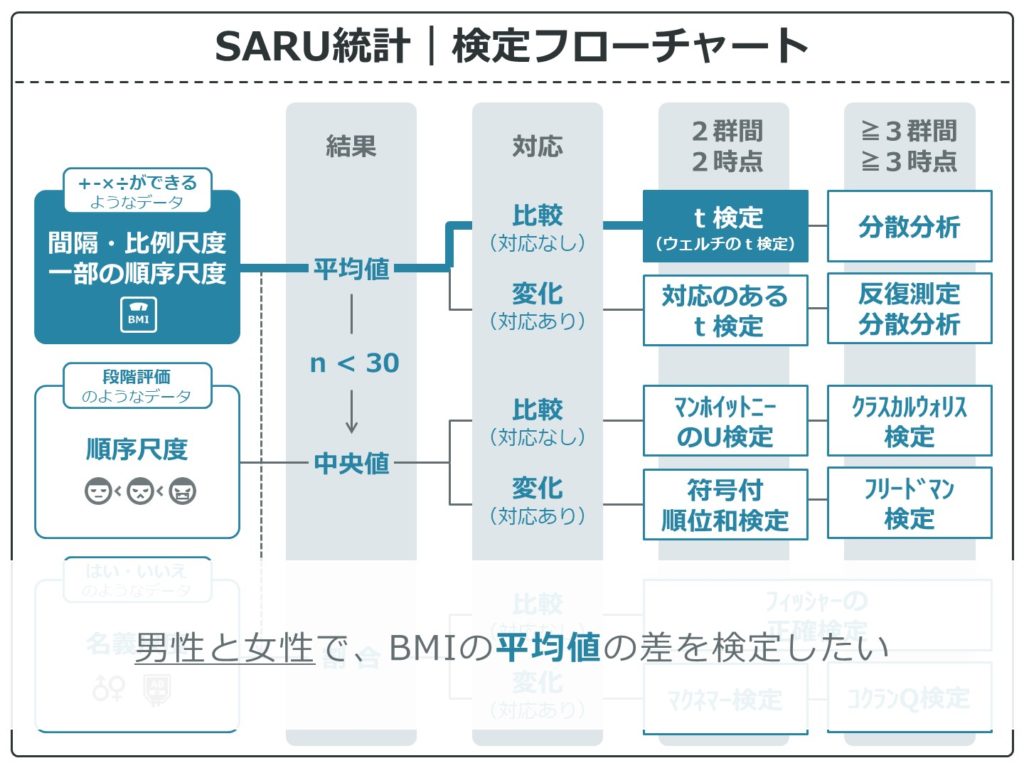
もし、3群以上の比較の場合は分散分析になります。
2グループ間比較で平均値or中央値の差

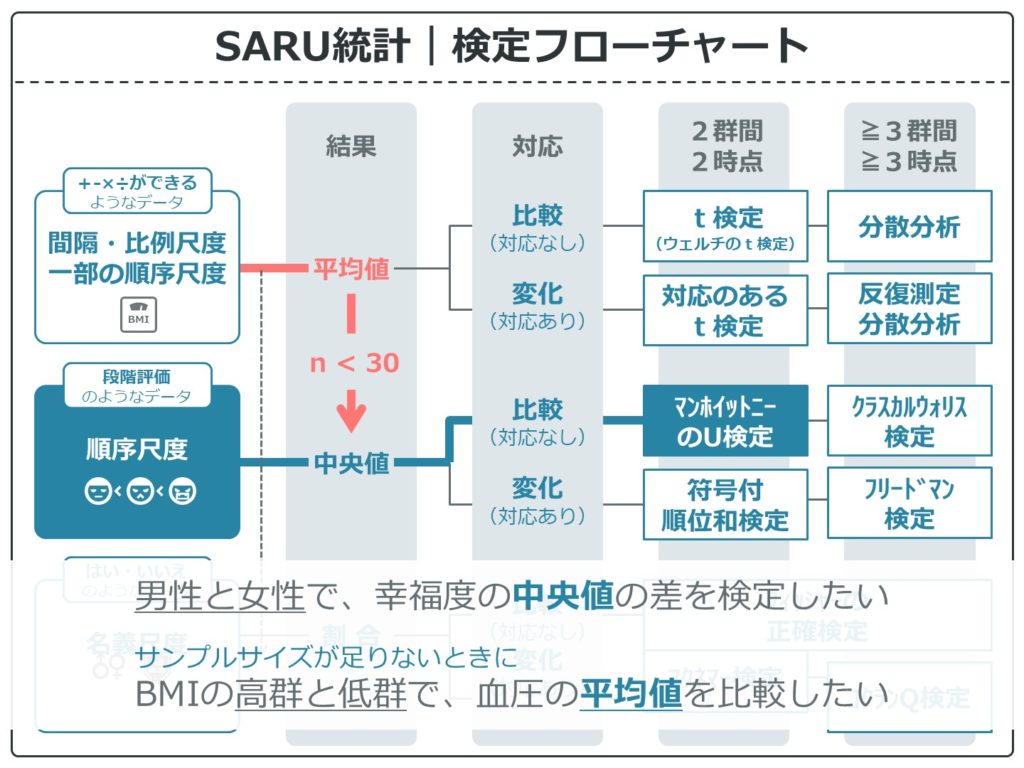
間隔・比例尺度でも、サンプル数が各グループ30未満の場合は、マンホイットニーのU検定の使用を推奨します。その場合、結果は平均値で示し、P値はマンホイットニーのU検定で計算することになります。
2時点間の変化で平均値の差
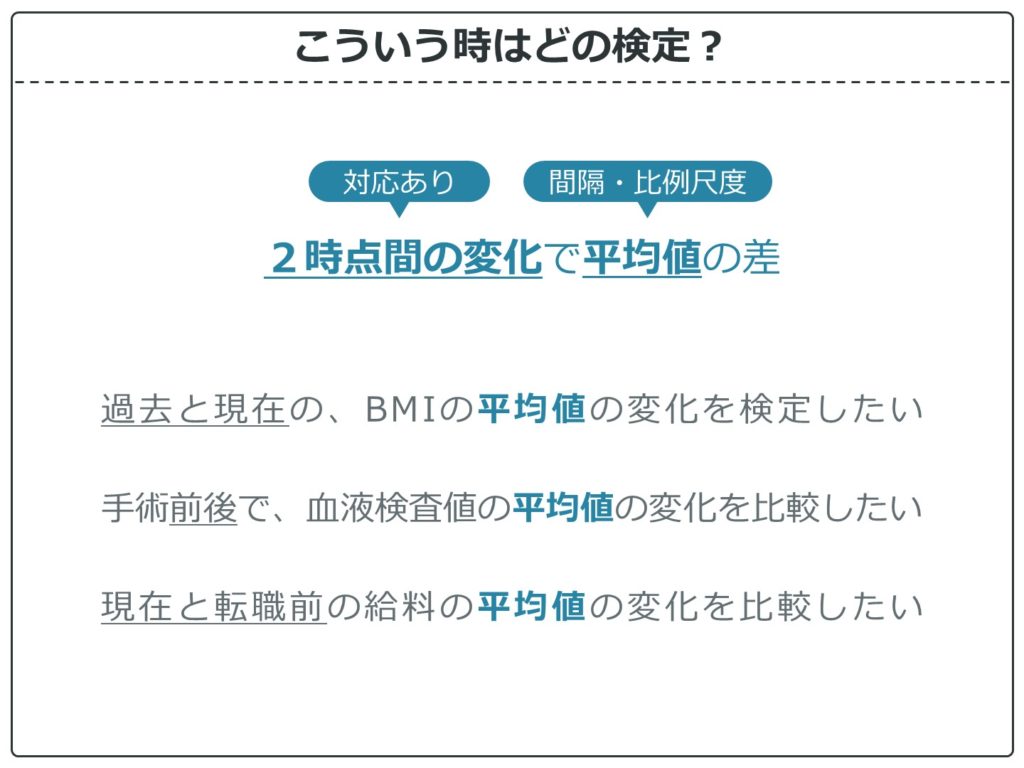

対応のところで、変化(対応あり)の方にフローを辿ります。3時点以上であれば反復測定分散分析を使います。
2時点間の変化で平均値or中央値の差
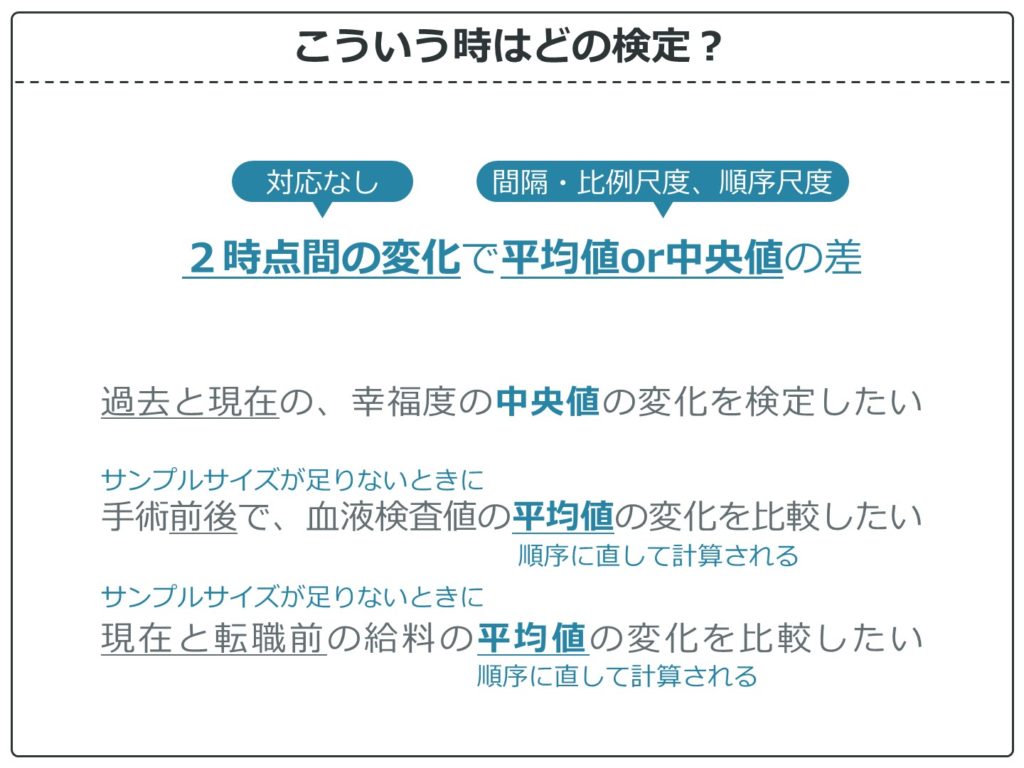
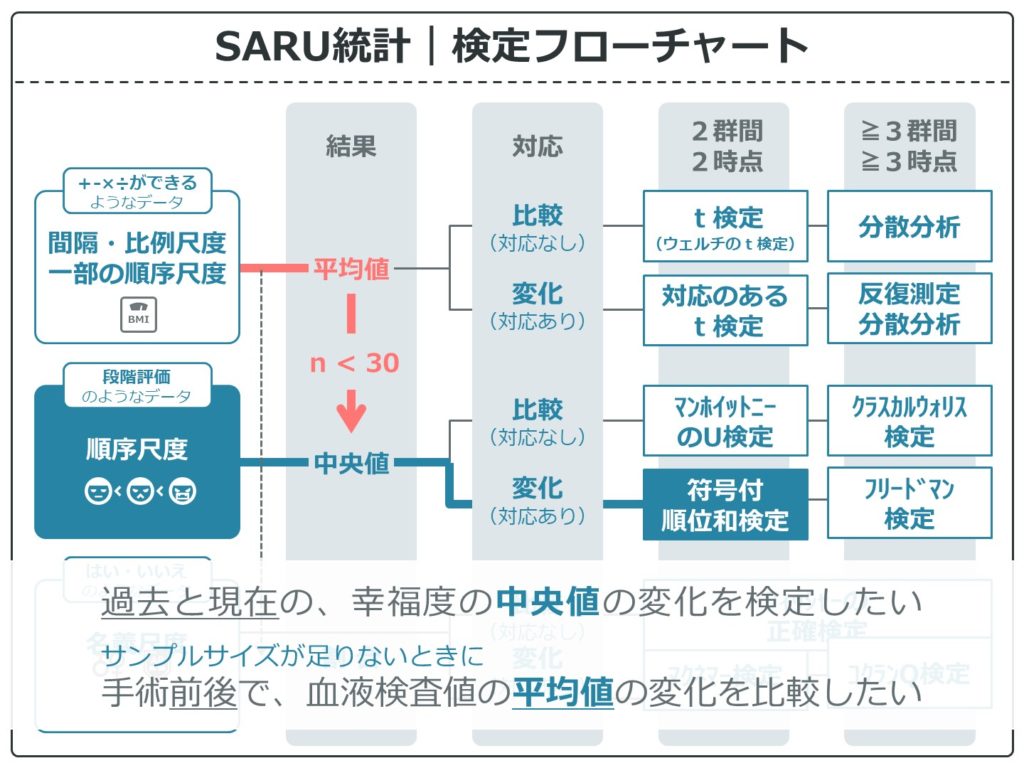
間隔・比例尺度でも、サンプル数が各グループ30未満の場合は、符号付順位和検定の使用を推奨します。その場合、結果は平均値で示し、P値は符号付順位和検定で計算することになります。
2グループ間比較で割合の差
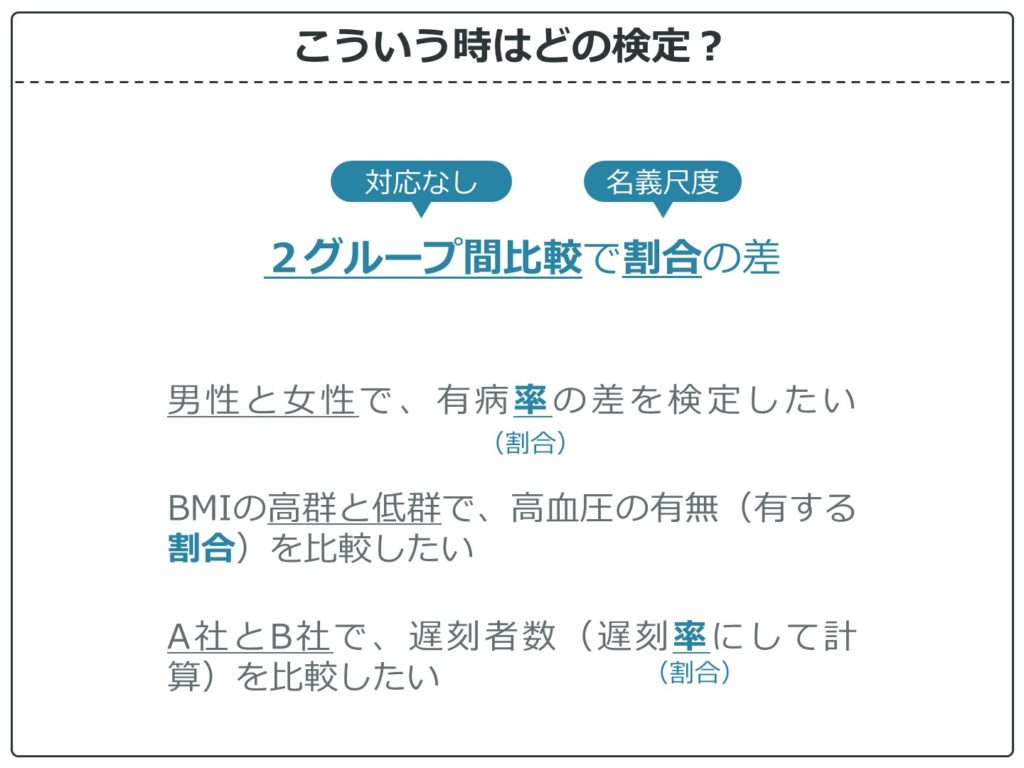
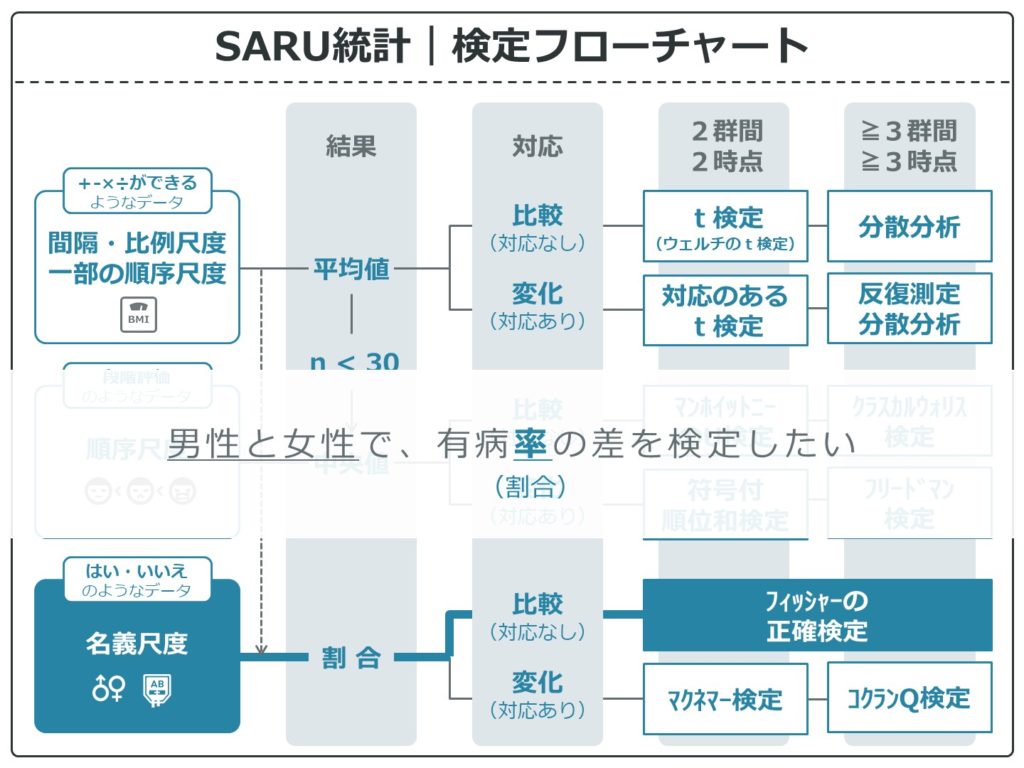
2群間でも3群間以上でもフィッシャーの正確検定を使います。
2時点間の変化で割合の差

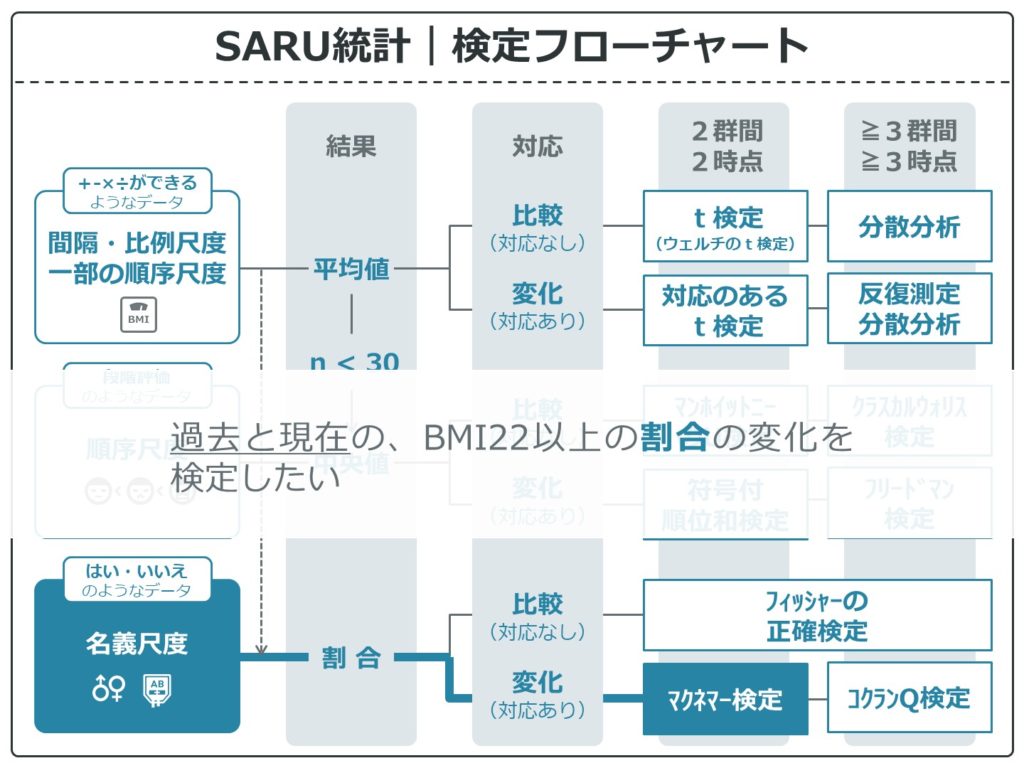
3時点以上で比較する時はコクランのQ検定を使います。
おまけ|サンプルサイズについて

フローチャートの中に出できたサンプルサイズについてです。ただ、ちょっと難しいので読み飛ばしても理解できなくても大丈夫です。
t検定、分散分析、対応のあるt検定、反復測定分散分析はパラメトリック検定といわれていて、使用する条件としてデータの正規性の過程が必要になります。
正規性があるかどうかは別の検定で調べることもできます。調べてから正規性がなければ別の検定を使うという流れもあります(※ただ、これは問題も指摘されています)
しかし、サンプルサイズが各30以上(2群間比較では計60以上)あれば、正規性の仮定をすることができるといわれているので、今回は初心者向けにサンプルサイズで使い分けるフローチャートになっています。
この方法は色々ある検定の使い分けの1つの方法だと思ってもらえればいいかなと思います。
まとめ

今回の記事をまとめておきます。
フローチャートとこのまとめのスライドを保存しておくと、困ったときにすぐに見れるかもしれないですね。
今回はここまでです。