私たちの関係って、なんなんでしょうね…

急にどうしたんですか?

目に見えないもどかしさ…

相関を調べれば、2つの関係性を目で見ることができますよ!

…。
2つの関係を見てみよう!
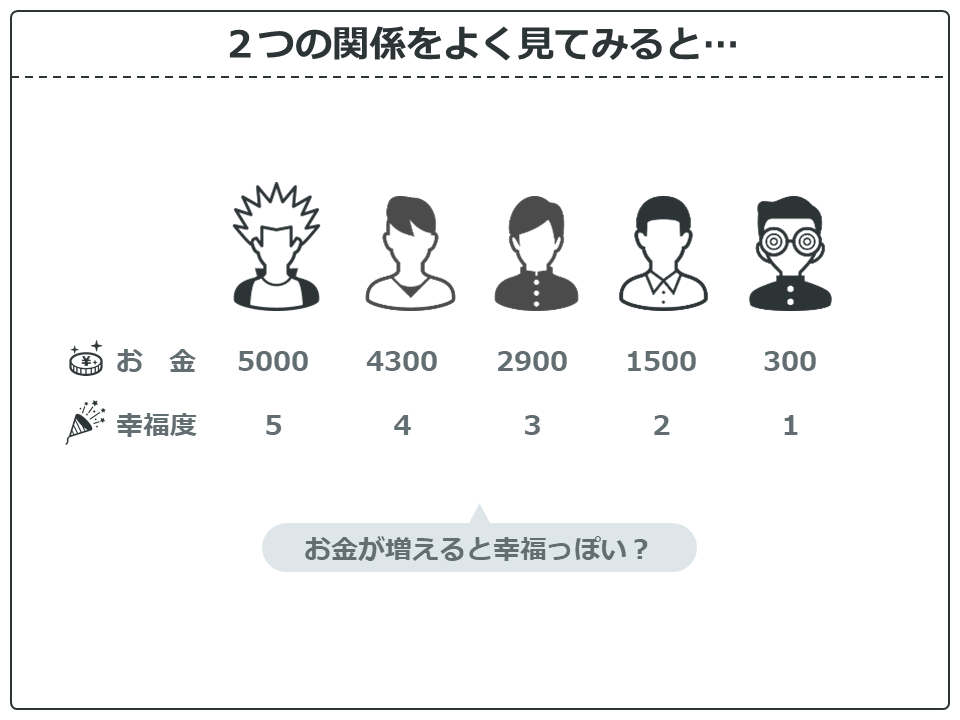
さて、5人の男の子たちがいます。陽キャっぽいこからちょっと地味目なこまで並んでいますね。
それぞれのお金をいくら持っているか、また幸福度は5段階でいくつになるか聞いてみました。そしてお金持ち順に並べてみると…
なんか、お金が増えるにつれて幸福度も高くなっている感じがしますね。
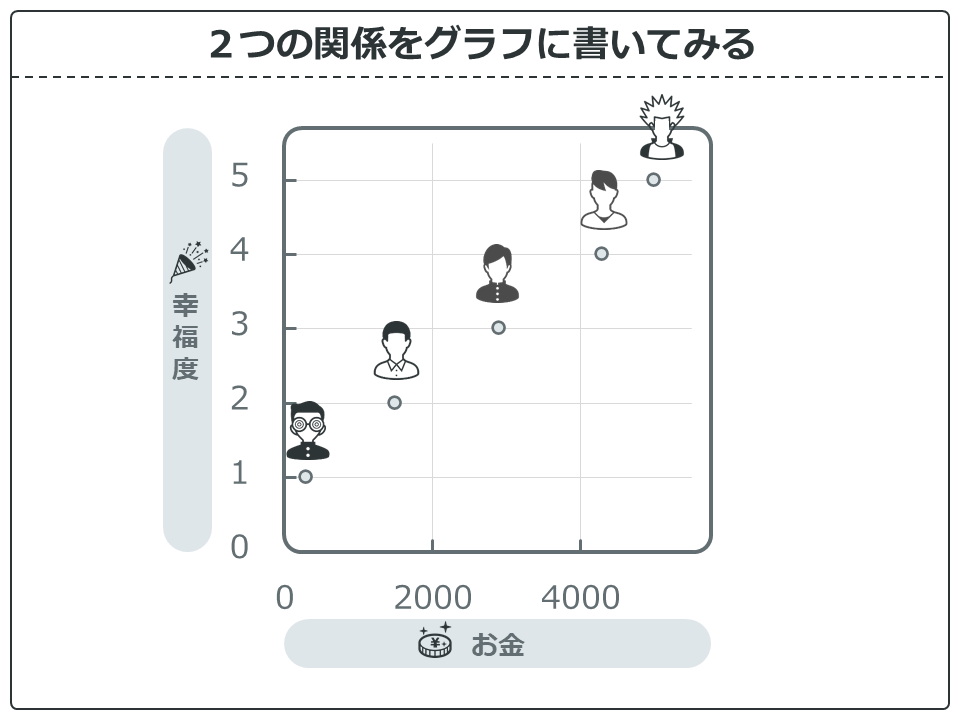
お金と幸福度、2つの関係をグラフにしてみました。こういったグラフの名前を散布図といったり相関図といったりします。
んー、やっぱりお金が増えると幸福度が高くなっているように見えますね!何か関係がありそうです。
相関と相関係数を理解しよう!
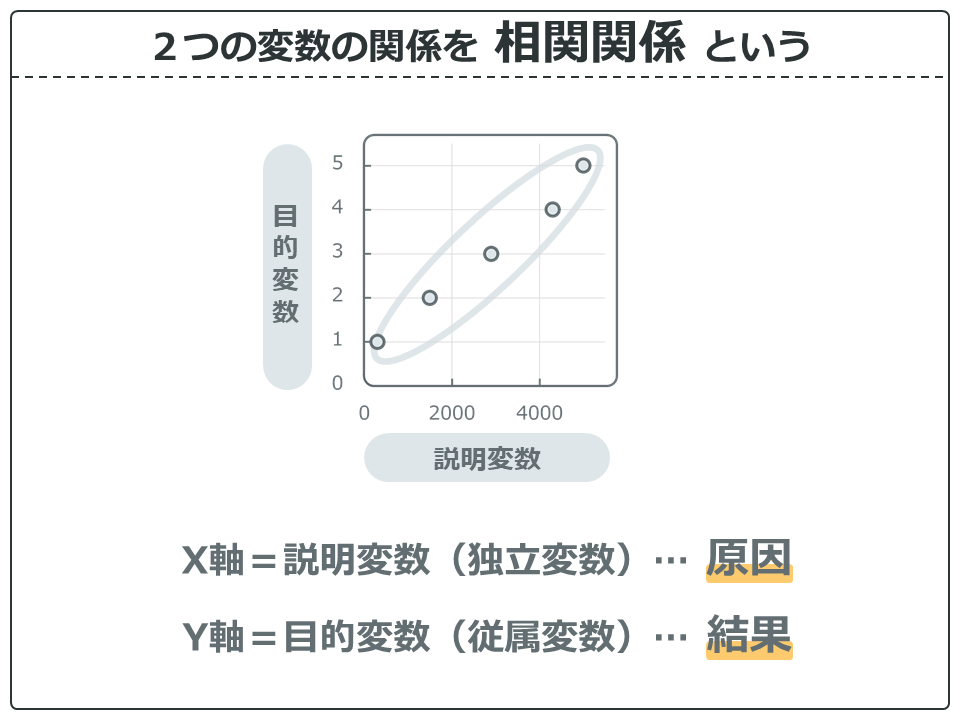
このように、2つの変数の関係を、相関関係と呼びます。また、グラフのX軸(横軸)を説明変数(独立変数)、Y軸(縦軸)を目的変数(従属変数)と呼びます。
また、こういった相関図ではX軸に原因、Y軸に結果となる変数をとることが一般的です。X軸に「お金」、Y軸に「幸福度」をとった場合、「お金が増えたり減ったりすることが原因で、結果として幸福度が増えたり減ったりする関係」というニュアンスになります。
余談なので読み飛ばしていいですが、結果=目的なのでY軸を目的変数と呼び、その原因を説明するのでX軸は説明変数といいます。また、Y軸はX軸の変化の結果なので、X軸の変化に依存=従属することになるので従属変数と呼ばれています。
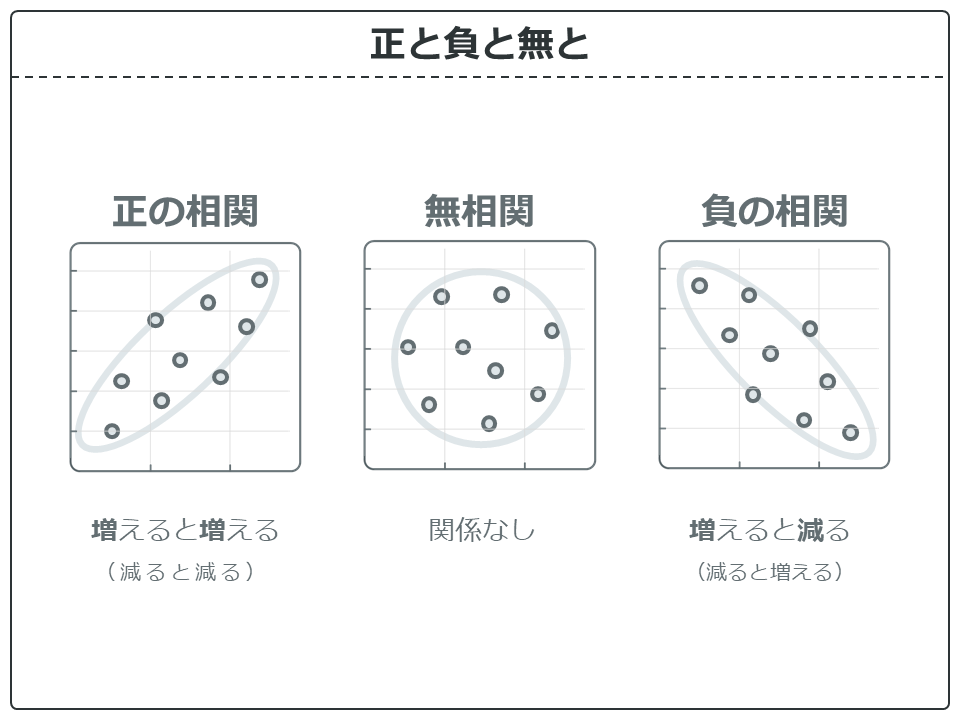
相関関係にはその方向性で、3つの呼び方があります。
正の相関は、増えると増える(減ると減る)関係で、グラフに書くと右上がりに分布します。
負の相関は、増えると減る(減ると増える)関係で、グラフに書くと右下がりに分布します。
そして、方向性がとくにない状態を、無相関と呼びます。
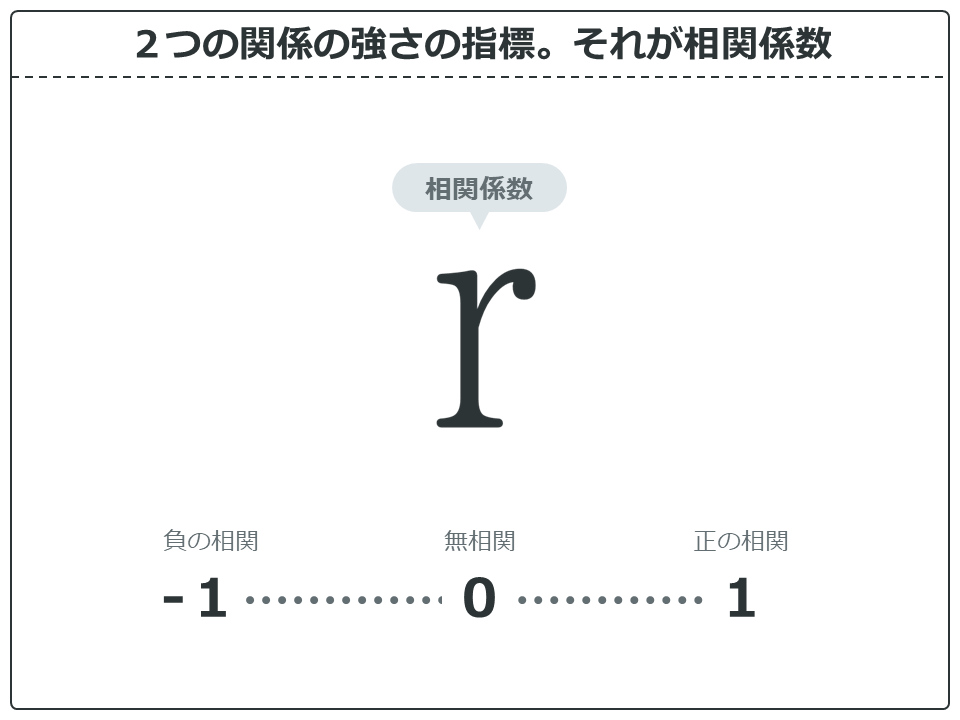
そして相関関係は、グラフで見るだけではなく数値としてみることもできます。相関関係を数値で示した値を相関係数(r)といいます。相関係数(r)は2つの関係の強さの指標です。
相関係数は0を中心に、最大+1、最低-1の範囲をとります。相関係数が0の場合は無相関となります。相関係数が正の値は正の相関、負の値は負の相関となります。
0を中心に左右対称なので、相関係数+1と-1は同じ相関の強さです。もちろん+0.5と-0.5も同じ強さです。つまり絶対値が同じであれば同じ強さですね。
相関係数の絶対値が0.3前後を弱い相関、0.5前後を中程度の相関、0.7前後を強い相関と表現したりします。しかし、これは研究のデザインに左右されてしまいます。
動物実験のように、実験環境を完全にコントロールできるような研究では相関係数は0.7は欲しいところです。反対に、人のように研究環境のコントロールが不完全な場合、0.3くらいでも上々と判断する場合もあります。このように研究分野で捉え方が違うので注意が必要です。おおまかに人は0.3、実験は0.7くらいに考えておいてもいいかと思います。
相関係数を扱う際の注意点
見かけの相関に注意せよ
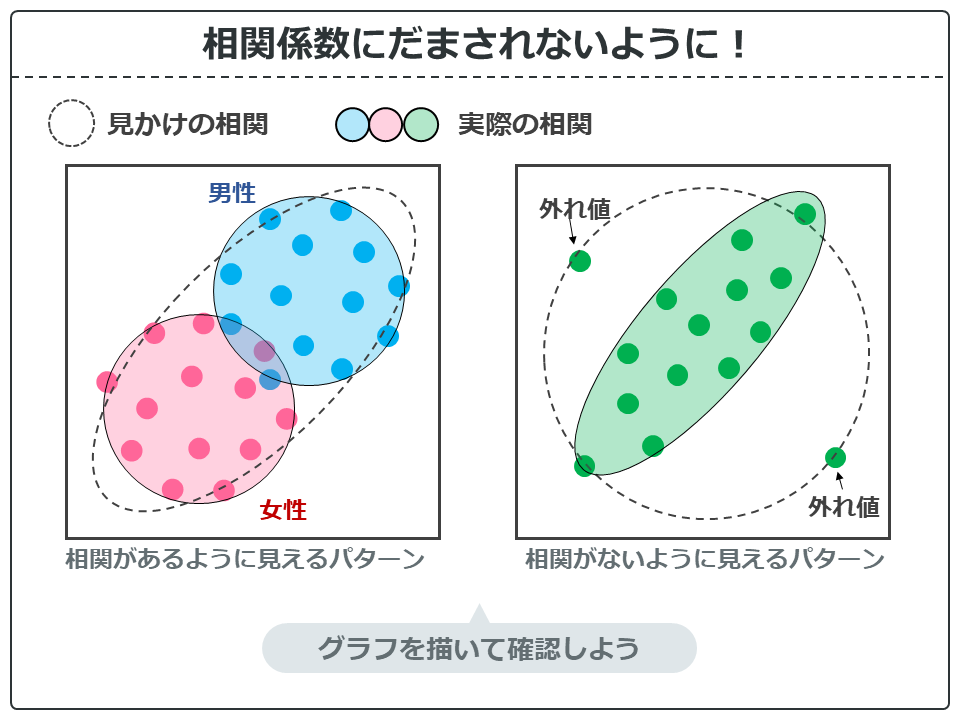
研究を行っていると、相関係数だけ計算して、だんだんめんどくさいのでグラフを描かなくなってきます。これちょっと注意が必要です。
上の画像を見てください。左のグラフは実際は相関がないのに相関があるように見えるパターンです。男女を分けずにみれば、正の相関があるように見えます。しかし、男女別に色分けしてみると、それぞれは無相関であることが分かります。
右のグラフは、実査に相関があるのに相関が無いように見えるパターンです。測定ミスなどで外れ値があるせいで、相関係数を計算すると0付近、つまり無相関になってしまいます。しかし、外れ値を除けば実際には正の相関があることが分かります。
このように、だんだんとめんどくさがってグラフは描かなくなってしまうんですが、グラフ化して目で見ることはとっても大切なんですね。
相関係数とP値は別で考えよ
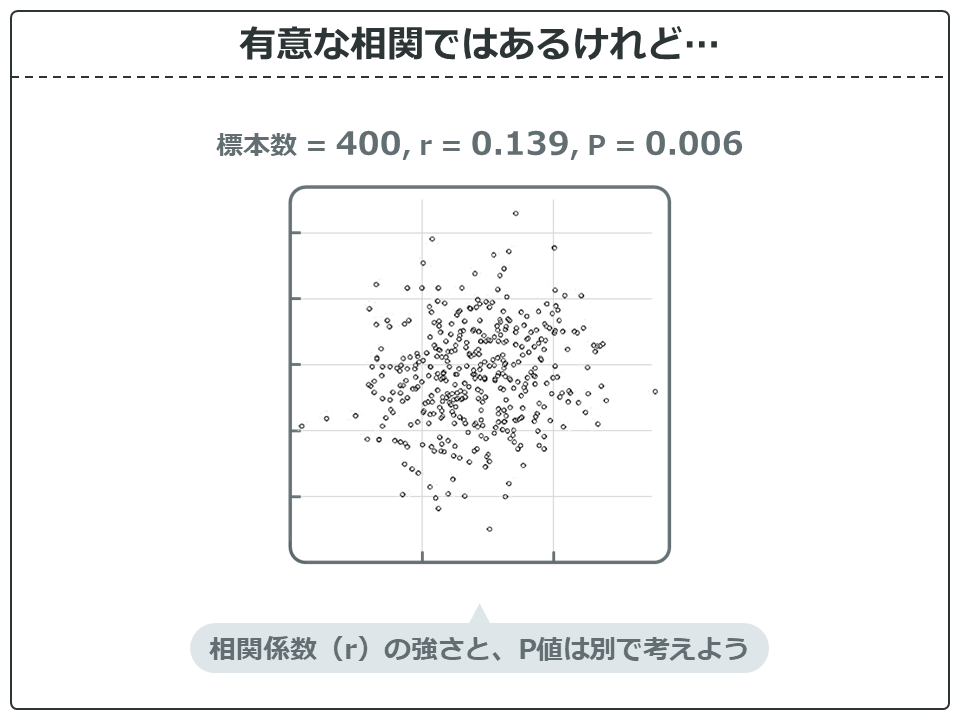
上のグラフは、相関係数(r)が0.139でP値が0.006と有意な相関です。
ですが、よく見てください。相関係数0.139ととても弱い相関ですし、正直グラフは無相関に見えます。でも有意な相関なんですね。
P値が小さくて有意な相関であっても、相関係数は小さいく弱い、むしろ無相関の場合があります。実は、これ標本数を増やせば増やすほど、どんな相関であってもP値が小さく出てしまうんですね。
このように、相関係数(r)の強さとP値は別で考えるようにしましょう。
因果関係に注意せよ
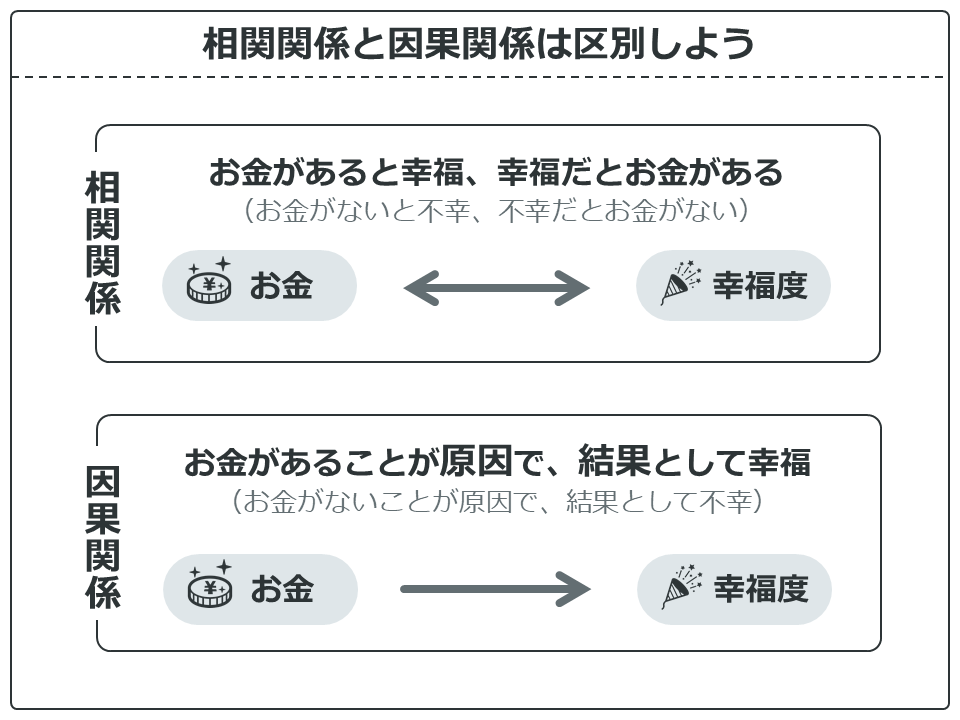
相関図の説明で、X軸は原因、Y軸は結果と説明しましたが、あくまでこれはニュアンスです。
相関関係と因果関係については、明確に区別して扱ってください。
相関関係は、関係を示す矢印が両方向に向いています。つまり、統計的にはどっちが原因でどっちが結果かははっきりしていないんですね。研究者はどっちが原因かある程度予測しているはずなので、グラフを描くときにX軸に原因っぽい変数を選択しますが、あくまで原因と結果の科学的根拠がない状態が相関関係です。
一方、因果関係は原因と結果がはっきりとわかっている状態です。
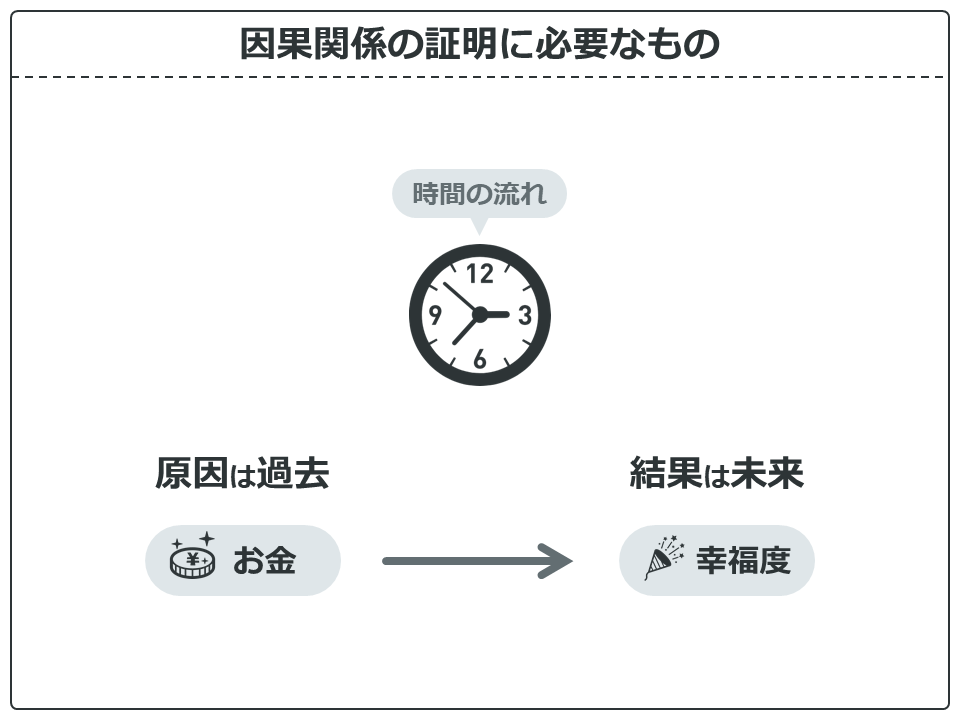
ではどうすれば因果関係を示せるのでしょうか?因果関係の証明には時間が必要になります。
ちょっと難しい話をしますね。
原因は過去にあるもので、その原因があるから未来に結果が生じます。このように時間の流れがあります。研究で因果関係を示すには、同じ対象を時間をかけて追跡調査する必要があります。縦断調査とも呼ばれます。
例えば、今お金が多い人と、少ない人がいたとします(=原因)。全員幸福度は中程度でした。この人たちを5年間縦断調査しました。5年前にお金が多かった人は5年後に幸福度が上がり、少なかった人は幸福度が下がりました(=結果)。この変化を測定することで因果関係を示すことができます。
反対に、今の時点でお金が多く幸福度が高い人と、今の時点でお金が少なく幸福度が低い人がいたとしても、どちらも今の時点のみしか調べていません。つまりお金が先か幸福が先か、どっちが先(原因)だったのかわからないんですね。この場合は因果関係は示せず、相関関係しかわかりません。
研究をまとめるときは、相関関係なのか因果関係なのかしっかりと区別してください。
まとめ(時間がない人はココだけ)
- 2つの関係を相関関係
- 相関の強さは相関係数(r)
- 相関係数は【-1~0~1】の範囲