
パーセントってなんか苦手なんです

食塩水の濃度の計算とかで挫折する人いますよね

うぅ…頭が

統計ではよく使うので、ひとつずつ整理して覚えていきましょう
数を数えて分類しよう!度数とそのまとめ方
統計解析でパーセントや割合って聞くと、頭痛や吐き気がする人いると思います。まぁ、あんまり難しく考えないように。数を数えて、まとめるだけです。
ちゃんと表にして、グラフに描けばそんなに難しいことはありません。
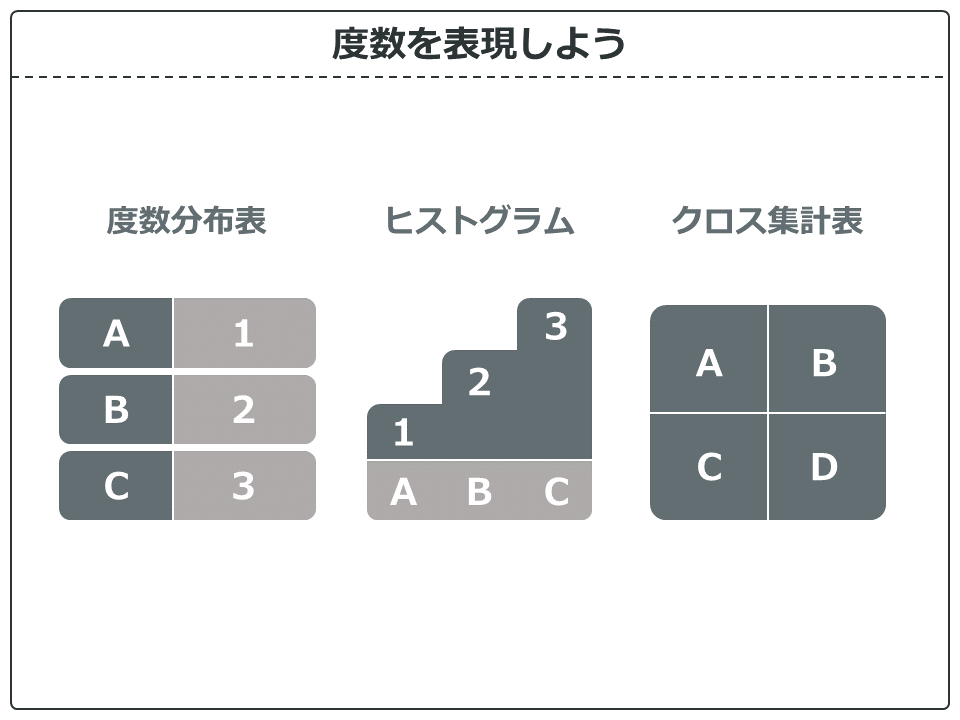
数を数える。その数のことを統計では度数と呼びます。度数にはいろいろな表現の方法がありますが、その中でも代表的な度数分布表、ヒストグラム、クロス集計表について見ていきましょう。
度数分布表について理解しよう
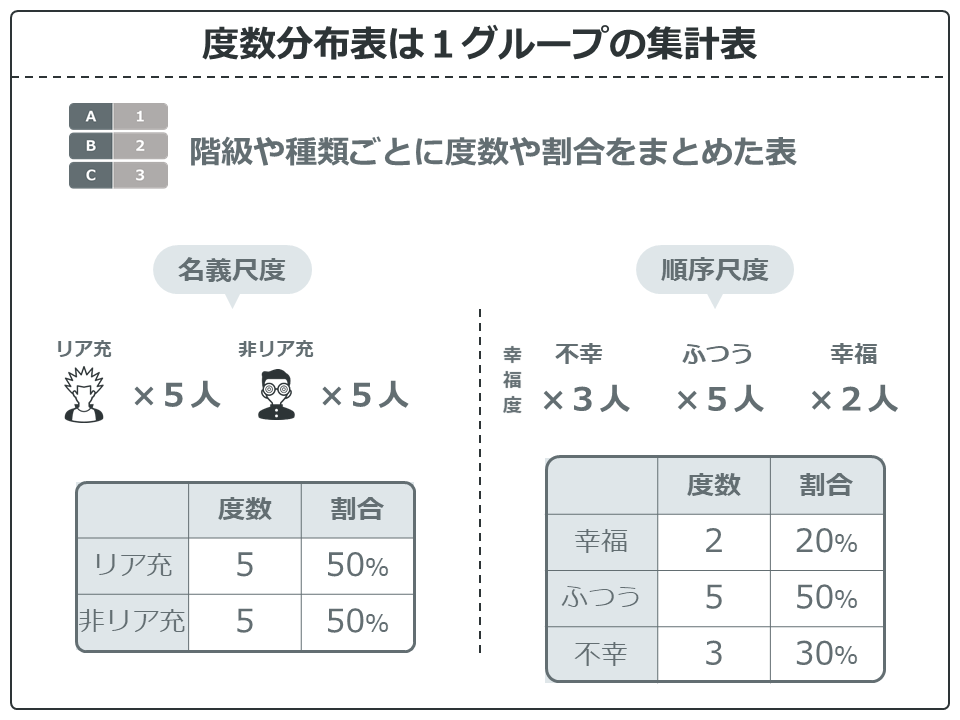
度数分布表は、1つのグループ、つまりグループ分けをせずにデータを集計するときに使います。
例えば、名義尺度の例では、リア充が5人と非リア充が5人いるので、それぞれの種類ごとに表にまとめてあります。また、表にまとめることで、その度数の全体に対する割合(%)も計算することができます。
順序尺度の例も見てみましょう。不幸、ふつう、幸福の3段階の階級があります。それぞれの度数を表にまとめることで、その階級の割合(%)も計算できます。
また、間隔・比例尺度を度数分布表にまとめるときは、任意の一定の幅の階級を作って度数をまとめます。例えばBMIであれば「18未満」「18以上20未満」「20以上22未満」「22以上24未満」「24以上」のように任意で階級を決めて度数分布表を作ります。この時、階級の幅はそろえましょう。この例でいえばBMI2ずつの区切りで階級が設定されています。
ヒストグラムについて理解しよう
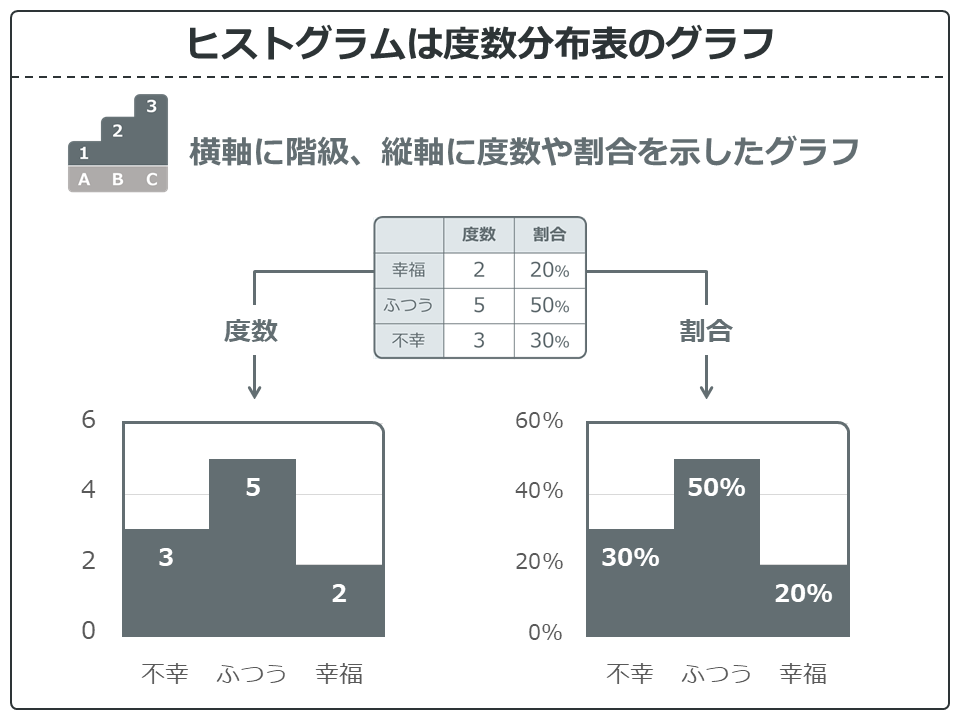
ヒストグラムは度数分布表を棒グラフにしたものです。グラフを描くときは縦棒と縦棒のすきまは無くしてくっつけましょう。そういうものです。ヒストグラムを描くことによって、全体の分布を把握できます。
ヒストグラムは度数をそのままグラフにしたものや、割合(%)をグラフにしたもがあります。
度数そのままヒストグラムは、実際の数を把握したいときに使います。ただ、注意点があります。母数(度数の合計)が違うと、ほかのヒストグラムと比較ができません。例えば、度数が5であっても母数が10に対する5なのか、母数が100に対する5なのかで、その意味合いは変わってきてしまいます。
割合にしたヒストグラムは、その欠点をカバーできます。10に対する5ならば50%ですし、100に対する5ならば5%です。このように、ほかのヒストグラムとも比較できます。度数と割合(%)を併記すればどちらも把握できるヒストグラムになります。
ちょいと難しい話。
ヒストグラムのグラフの面積は、度数や割合(%)を示しています。度数のヒストグラムであれば総面積=総人数ですし、割合のヒストグラムであれば総面積=100%になります。半分の面積に半分の度数が存在することになります。ヒストグラム=面積のグラフなので、グラフとグラフのすきまは無くしてくっつけるってことなんです。
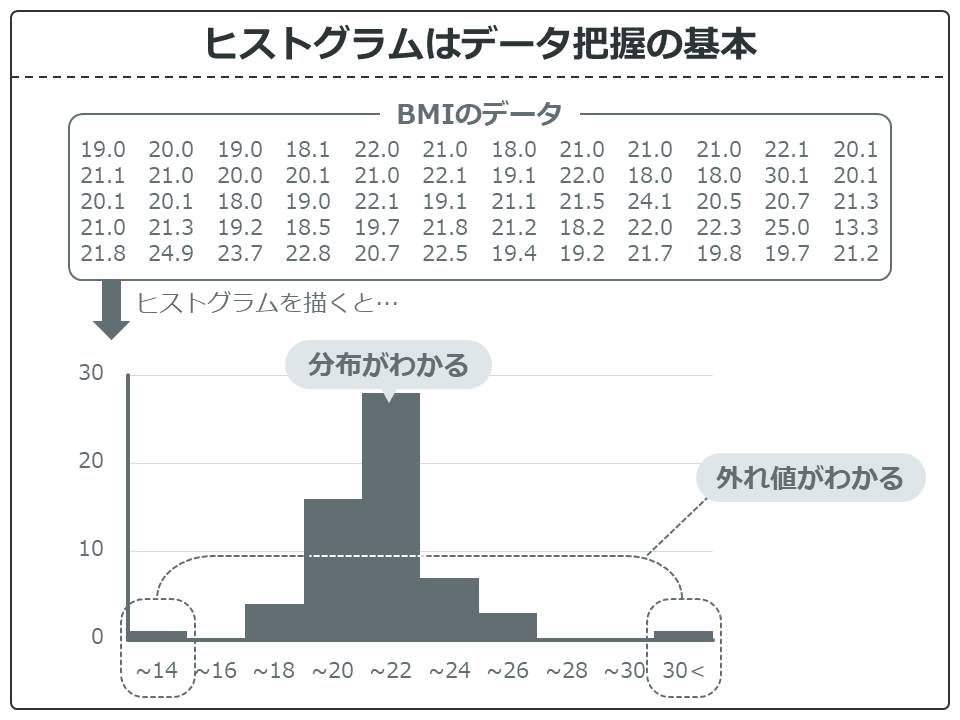
ある程度統計を勉強していれば、ヒストグラムなんかなくても、平均値とそのばらつきの標準偏差でだいたいの分布は把握できます。
しかし、ないがしろにしがち(私もそうです)ですが、ヒストグラムを描いて分布を確認することはデータ把握の基本です。
上の画像のBMIデータを見てください。BMIの平均値±標準偏差を計算すると20.7±2.3なので、まぁBMIの範囲の中心は17~23くらいかなぁ~とは想像がつきます。でも、よく上のヒストグラムを見てください。
そんなんです。
ヒストグラムを描くことによって、全体の分布の把握だけではなく、外れ値の存在にも気づくことができるんです。だから、ヒストグラムはデータ把握の基本なんですね。
クロス集計表について理解しよう

最後はクロス集計表です。これは、度数分布表をさらにグループで分けたような表です。
上の例では、性別(男女)の度数を、さらにリア充と非リア充のグループで分けて集計したものです。縦と横でクロスして集計するのでクロス集計表と呼ばれます。
一般的に、グループや原因は行に、結果は列に分類します。ただ、統計ソフトによっては、原因と結果の行列を入れ替えて集計する場合もあるので、どちらでも読めるようにしておきましょう。
それぞれの行・列の最後に合計を記入し、右下には総合計を記入します。総合計=全標本数になります。
また例のように原因2つ結果2つの表を、2×2のクロス集計表と呼びます。もちろん、2×2よりも大きなクロス集計表を作成することができます。
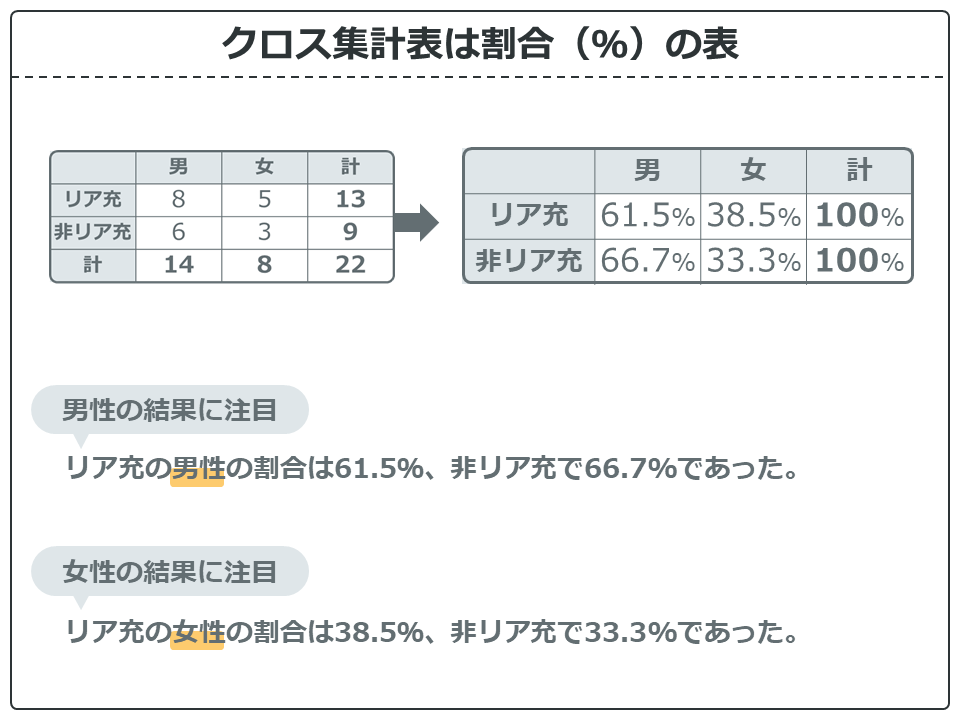
そして、クロス集計表からそれぞれの割合を計算することができます。計算する方向を間違えないようにしましょう。
この例ではリア充と非リア充で比較しているので、行(横)方向に計算しています。リア充は全部で13人いて、そのうち8にんが男なので8÷13=61.5%といった具合ですね。

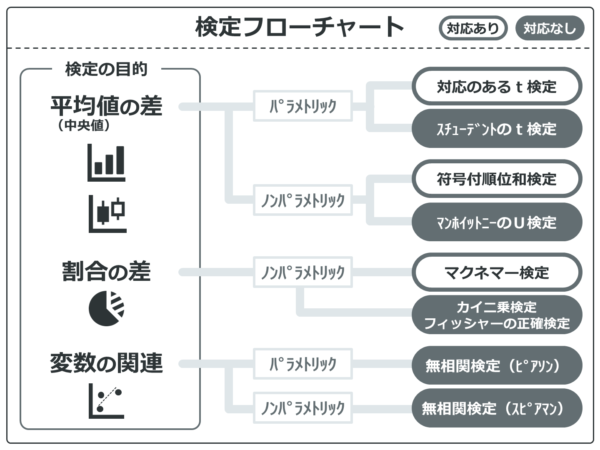
クロス集計表から求めた割合の差は、検定することで偶然かどうか調べることができます。検定がピンとこない人は下記の記事を参考にしてください。
対応がないデータについてはカイ二乗検定か、フィッシャーの正確検定を用います。
また、対応があるデータであればマクネマー検定を用います。
以下、難しいけど大切なことなのでよく理解してください。
2×2のクロス集計表の場合、割合の差は2パターンあります。先ほどの例であれば、1つめは「リア充と非リア充の男性の割合の差」、2つめは「リア充と非リア充の女性の割合」の差です。
しかし、男性の割合と女性の割合って、どっちかを計算したらもう一方の値は確定しますよね?男性が70%なら女性は絶対30%になります。このように表裏一体となります。
なので、差についてもよく見てみると、男性は61.5%と66.7%なので5.2%の差ですし、女性も38.5%と33.3%なので5.2%の差です。
つまり、2×2のクロス集計表の場合、割合の差のパターンも表裏一体となるので1通りの差について検定すれば済むんですね。
では、性別が「男」と「女」と「その他」の3つに分かれたとしましょう。リア充の「男」が70%だとしても、残りの「女」と「その他」の割合は確定しません。表裏一体とならないので、差の検定をするときも、すべてのパターンを検定しなければなりません。この場合、リア充と非リア充で「男の差」「女の差」「その他の差」の3パターン検定をする必要があります。
ここで問題があります。
カイ二乗検定、フィッシャーの正確検定、マクネマー検定の検定結果のP値は1つしか計算されません。2×2のクロス集計表であれば、1つ計算できれば表裏一体なので問題ありません(どちらも同じP値になる)。しかし、差が3パターンあった場合、P値が1つしかないので「3パターンの差のどこかに有意差がある」までしかわからず、「どことどこの差に有意差があるかはわからない」という結果になってしまいます。
これを解決する問題は2つあります。
1つめは「その後の検定」というひとつ踏み込んだ統計解析をさらに行う方法。そして2つめはどんなデータも2×2のクロス集計表にする方法(統計初心者は断然おススメ)です。
2つめについては、「男」「女」「その他」であれば女とその他をまとめて「男」と「その他」で検定する。幸福度のように例えば5段階(5:幸福、4:やや幸福、3:普通、2:やや不幸、1:不幸)もあれば、「4以上」の幸福グループと「3以下」のその他グループに分けて集計して検定するといった具合です。
とりあえず、よくわからなかったら2×2のクロス集計表になるようにしましょうってことですね!
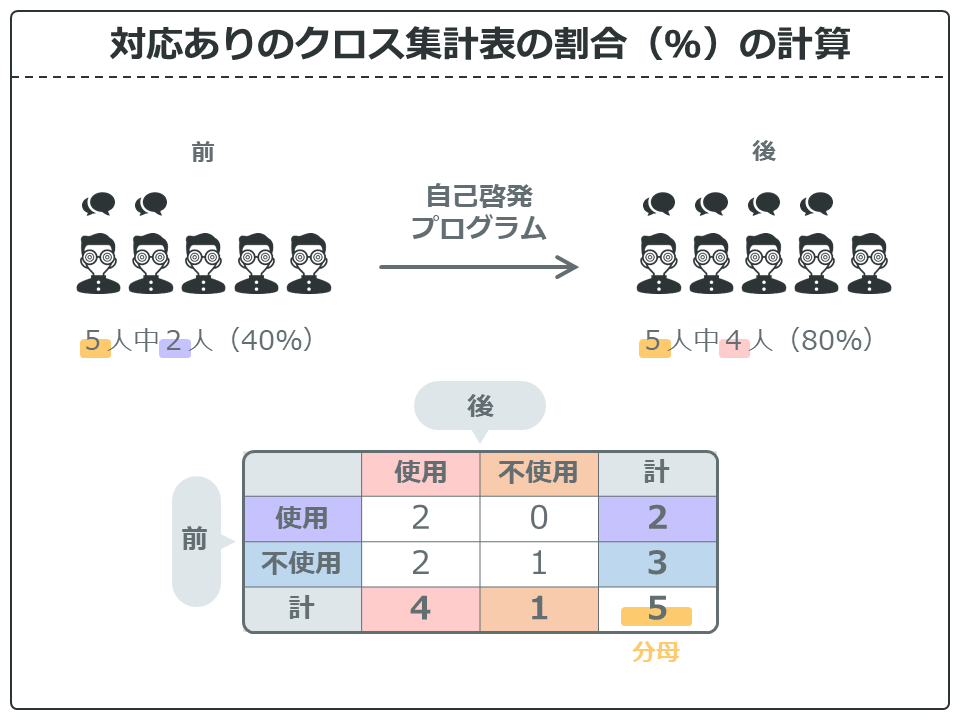
最後はよく頭がこんがらがりやすいことを紹介しときますね!
対応のあるクロス集計表を作成したときの、表の見方と割合(%)の計算方法です。上の例では、自己啓発プログラム実施前と実施後のSNS使用についてまとめてあります。
対応のないクロス集計表は行(横)方向ごとに計算していましたが、対応のあるクロス集計表では、「計」のところにある数値を使います。
例えば実施前のSNS使用割合は、行(横)方向の「計」の2を「分母(総計)」の5で割って求めます(40%)。そして、比較対象の実施後のSNS使用割合は列(縦)方向の「計」の4を「分母(総計)」の5で割って求めます(80%)。不使用であればこの反対で計算できます。
対応ありのクロス集計表の割合の計算は、本当に頭がこんがらがるので注意してくださいね!
まとめ(時間がない人はココだけ)
- 度数分布表は度数の集計
- ヒストグラムで分布と外れ値
- クロス集計表はグループ集計
- クロス集計表は2×2にする
- 検定はカイ二乗検定、フィッシャーの正確検定、マクネマー検定