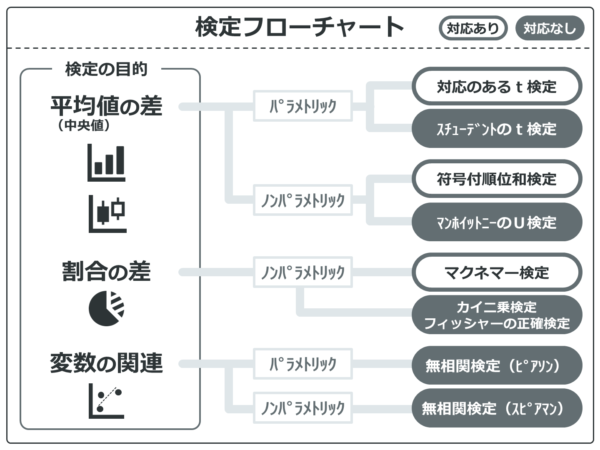
何か急に難しいヨコモジでできました!

初めて聞く人も多い言葉ですね

もしかしてパラパラと関係してます?

関係ないです。踊ったりしません。でも振り付け覚えるよりは簡単ですよ!

…なんだぁ

と、とりあえずダンスも統計も練習あるのみです!
そもそも検定ってなんだろう?
さて、この記事のタイトルにもパラメトリック検定というように検定という言葉があります。統計解析を調べているとこの検定という言葉をよく目にすると思います。
難しく言えば、「検定は仮説を立て、その仮説が成り立つ確率を求めて、結論を導き出す」作業です。でもまぁそんな難しいことはあんまり考えないでください。
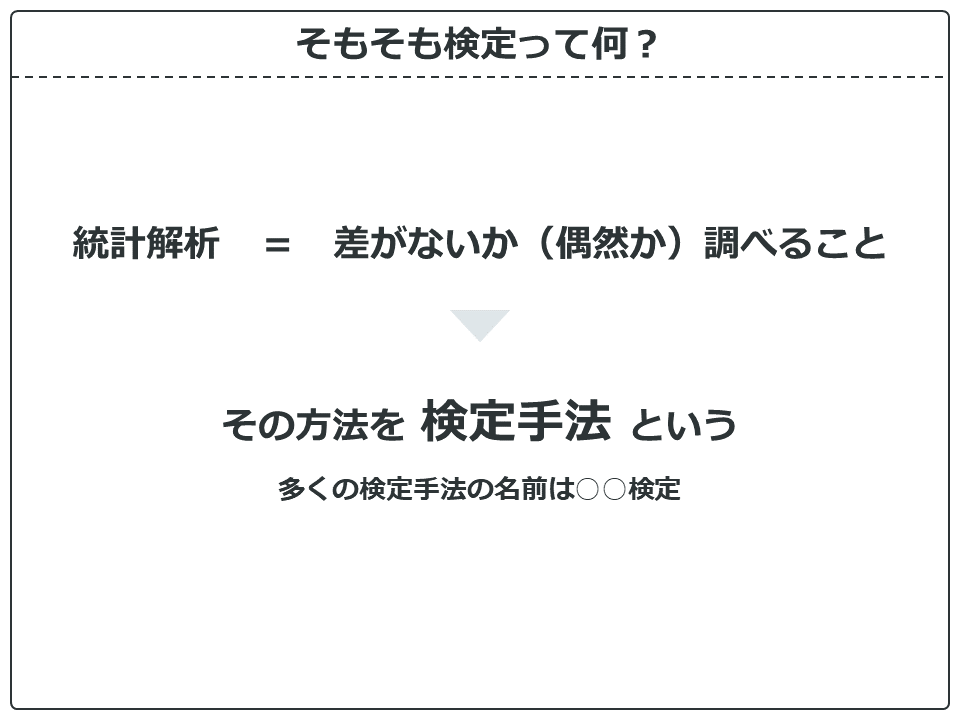
簡単に言えば、2つ(以上)のグループ間に差がないか(偶然か)調べる方法を検定手法といいます。世の中には様々な検定手法がありますが、たいてい〇〇検定という名前です。
そして、上の画像を難しい言葉に当てはめるなら、「仮説を立て」の仮説が「差がない」の部分、そしてその「差がない」確率を計算するのが検定になります。ややこしいですが、「差がない」確率が小さければ、反対に差があるということになるんですね。すべての検定は、方法は違えどやってることはすべてこれだけなんです。
ここは、今は理解できなくても大丈夫です。別の記事でしっかりとお伝えします。
パラメトリック検定とノンパラメトリック検定
それではパラメトリック検定とノンパラメトリック検定についてみていきましょう。
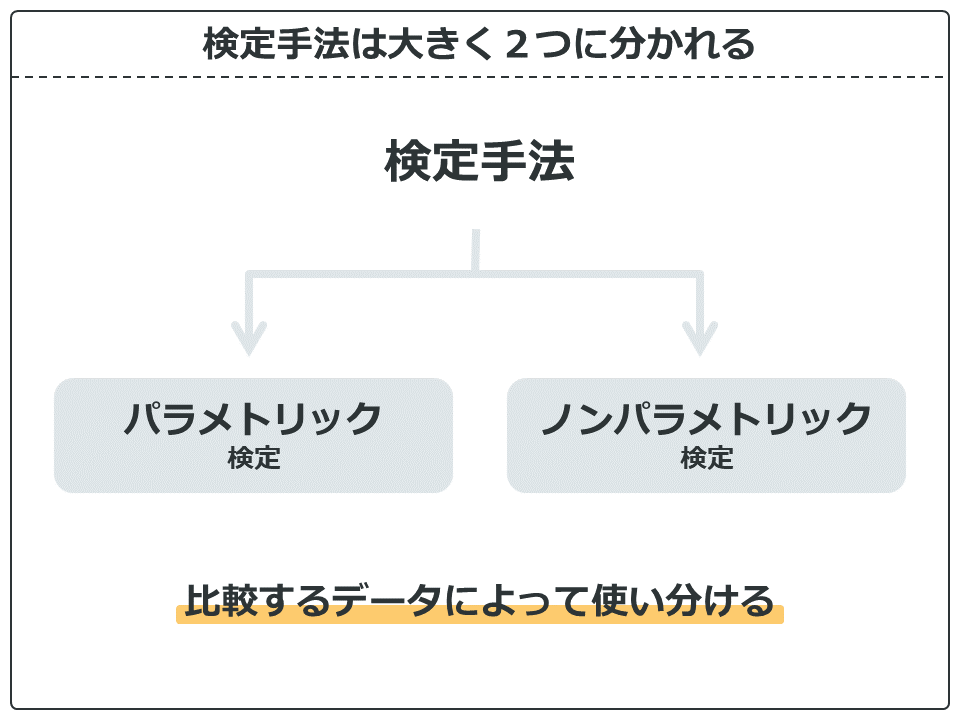
検定手法は大きくパラメトリック検定とノンパラメトリック検定のどちらかに分かれます。パラメトリック検定やノンパラメトリック検定は検定手法というより、検定の分類となります。
そして、比較するデータの性質によって使い分けることになります。次の表では、使い分けの方法をまとめてあります。表にある尺度と基本統計量については別の記事で詳しく説明しているので、よくわからない方は先に読んでおくことをお勧めします。

順番に見ていきましょう。
まず尺度について。必ず覚えてください!パラメトリック検定は間隔・比例尺度しか使えません。ノンパラメトリック検定はどんな尺度でも大丈夫です。
基本統計量と母集団の仮定は、ホントはきちんと勉強したほうがいいのですが、初心者には荷が重いです。とりあえず今は、パラメトリック検定はいろいろ条件があるのに、ノンパラメトリック検定は不問ということを覚えましょう。
続いて、標本数(?)です。パラメトリック検定は1グループあたり30以上必要と覚えておきましょう。男性グループと女性グループの2グループの比較なら60以上、3グループなら90以上です。これにも統計的な根拠がありますが、難しい話なので割愛します。ノンパラメトリック検定は、またまた不問です。
そして、一番大切なのが信頼性です。統計の言葉では検出力といいます。とりあえず、パラメトリック検定の方が検出力高いので、真実に近い結果が得られます。ノンパラメトリック検定は何でもOKの万能検定に見えますが、信頼性は低いです。できる限りパラメトリック検定で検定を行うようにすることを覚えておいてください。
まとめ(時間がない人はココだけ)
とりあえず、これだけ覚えておきましょう。また、確認問題で学んだことを確かめてみてください。

- 間隔・比例尺度で30以上:パラメトリック検定
- それ以外:ノンパラメトリック検定