本記事ではExcelだけで統計解析を行っていきます。しかし、Excelで統計解析しても論文や学会発表では使えません。そんな悩みを少しでも解消できるツールを作りました！よかったら使ってください。
ダウンロードしていない方は、下記からE統計とデータをダウンロードしてください
それぞれの説明が必要な場合は下記からどうぞ
エクセル（E統計）でやるマンホイットニーのＵ検定
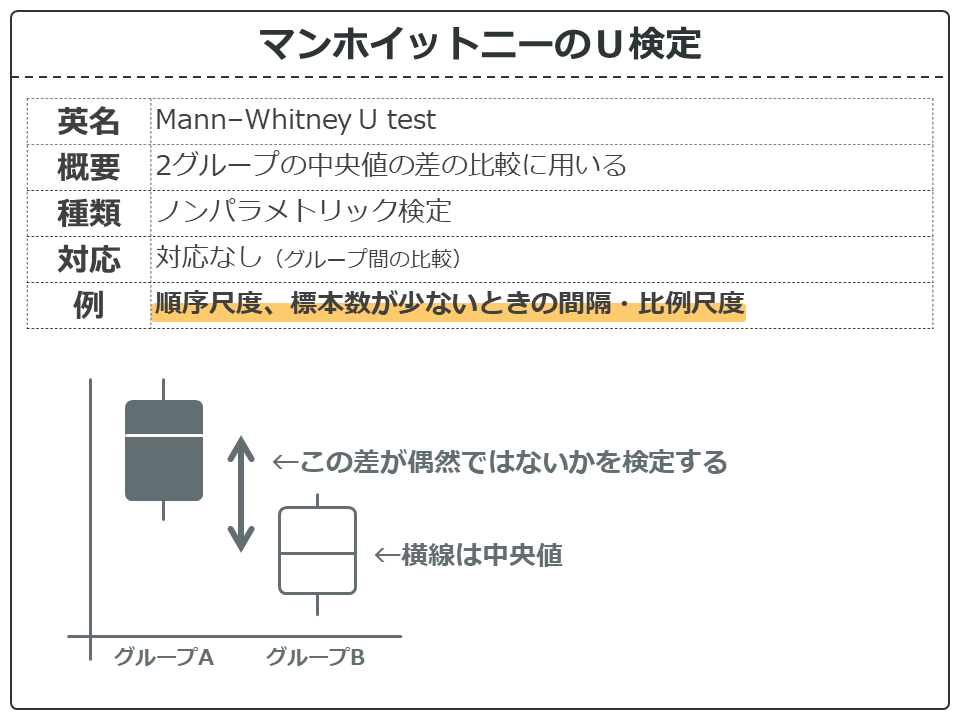
検定手法の概要です。マンホイットニーのＵ検定は対応のない中央値の差の検定を行うノンパラメトリック検定です。
では、「対応なしデータ」の基本統計量の表を見ながら、どこにマンホイットニーのＵ検定が適用できるか確認していきましょう。
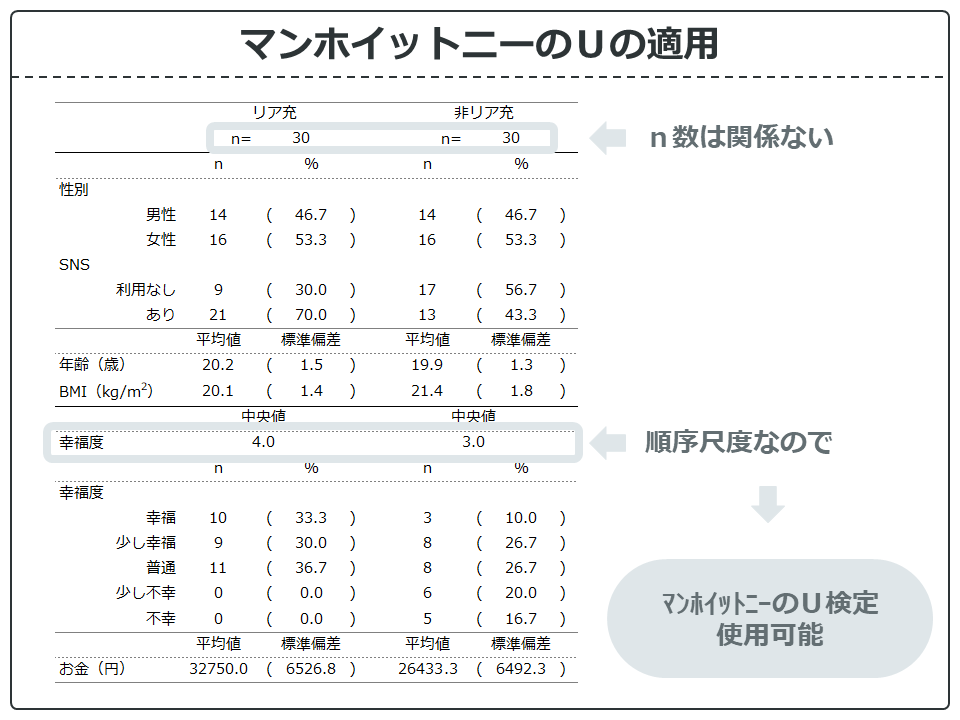
ノンパラメトリック検定なのでｎ数はとくに関係はありません。
また、ノンパラメトリック検定なので順序尺度でも間隔・比例尺度でも使えます。この場合「幸福度」はマンホイットニーのＵ検定で検定します。
ただ「年齢」と「BMI」は間隔・比例尺度なので、マンホイットニーのＵ検定が使えなくもないですが、ｎ数が十分いるのでパラメトリック検定のスチューデントのｔ検定を使用しましょう。ｎ数が少なければ、「年齢」や「BMI」などの間隔・比例尺度はマンホイットニーのＵ検定を使用します。
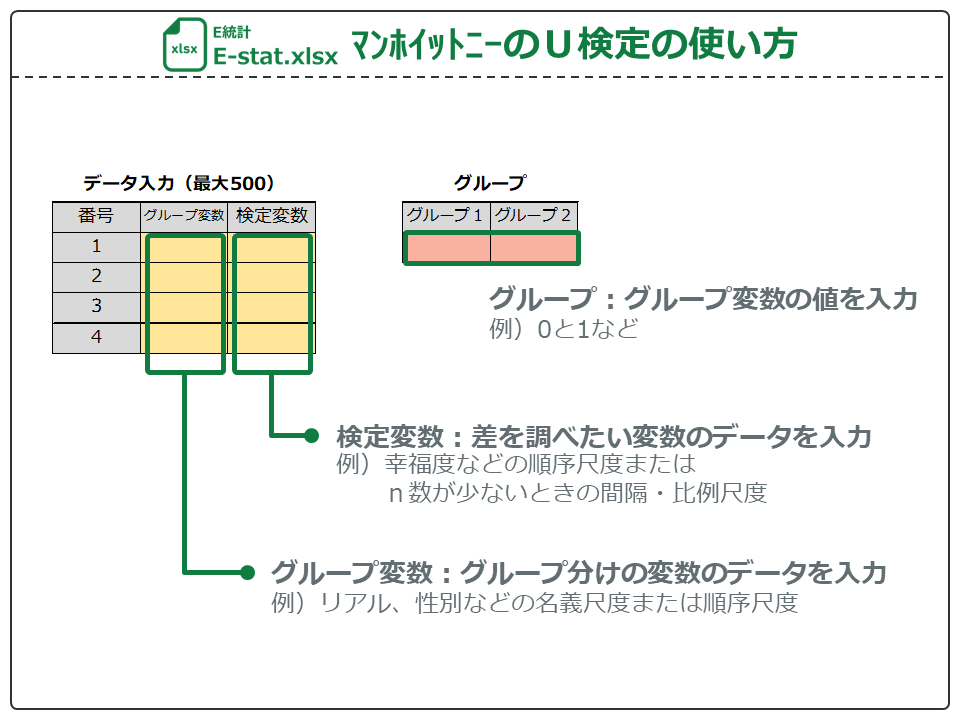
E統計のマンホイットニーのＵ検定の使い方です。
グループ変数にはグループ分けの変数のデータを入力します。「対応なしデータ」の場合、リアルや性別の名義尺度が入ります。また、幸福度の順序尺度を入力して、不幸グループと幸福グループで検定することもできます。
グループ変数を入力したら、グループ１とグループ２にグループ変数の値を入力します。「対応なしデータ」の場合、リアルの変数はリア充は０、非リア充は１となっているので、それぞれ０と１を入力します。幸福度のような順序尺度（１～５）は、比較したいグループの数値を入力します。例えば不幸グループと幸福グループを比較したいときはそれぞれ１と５を入力します。
検定変数には、差を調べたい変数のデータを入力します。「対応なしデータ」の場合、順序尺度の幸福度を入力します。
E統計にデータをコピペするときに、値貼り付けを行うと、書式を崩すことなく貼り付けることができます。
もし、書式を崩してしまったり、間違えて変なところを消したり編集してしまった場合は、また新しいファイルをダウンロードしてください。これが一番確実ですね。
それでは、リア充と非リア充の幸福度の差を検定していましょう！「対応なしデータ」から上記の手順で「E統計」に数値をコピペしてみましょう！
それでは結果を見てみましょう。グループ０はリア充、グループ１は非リア充ですね。幸福度は順序尺度なので中央値を見ます（ｎ数が少ないときの間隔・比例尺度は平均値を見る）。差は1.0でP値は0.002（0.2%）と有意水準0.05（5%）を下回っているので、有意差ありと判断できます。
論文等では「リア充の幸福度の中央値は4、非リア充は3であり、非リア充で有意に小さい値であった（P = 0.002）」と表現することができます。
さらに挑戦してみよう！マンホイットニーのＵ検定
さて、もう少し練習してみたいという人は、下記からファイルをダウンロードしてください（ほか記事のE統計練習用ファイルと同じです）
使用するデータセットは同じです。
